
Descriptive Statistics: Definition, Overview, Types, and Examples
Sep 21, 2024 7 Min Read 2510 Views
(Last Updated)
Have you ever wondered how researchers make sense of large datasets? Enter descriptive statistics, a powerful tool that helps you summarize and interpret numerical information.
This branch of statistics allows you to distill complex data into manageable insights, giving you a clear picture of what your numbers really mean. Whether you’re analyzing survey responses or tracking sales figures, descriptive statistics provides the foundation for understanding and presenting your data effectively.
In this article, you will learn about descriptive statistics and explore its various types. You’ll learn about measures of central tendency and variability, and see how these concepts apply to both univariate and bivariate data, and their examples.
Table of contents
- Understanding Descriptive Statistics
- Key Components
- Importance in Data Analysis
- Types of Descriptive Statistics
- A) Frequency Distribution
- B) Central Tendency
- C) Variability
- Univariate vs. Bivariate
- Univariate Analysis
- Bivariate Analysis
- Visualizing Descriptive Statistics
- Histograms
- Box Plots
- Scatter Plots
- Bar Charts
- Applications of Descriptive Statistics
- Business and Finance
- Healthcare and Medicine
- Education
- Social Sciences
- Concluding Thoughts...
- FAQs
- What is descriptive statistics and its types?
- What is the overview of statistics?
- What is the main purpose of descriptive statistics?
- Who is the father of statistics?
Understanding Descriptive Statistics
Descriptive statistics is a branch of statistics that helps you summarize, organize, and present data in a meaningful and concise way. Its primary goal is to provide a clear summary of a dataset’s main features and characteristics.
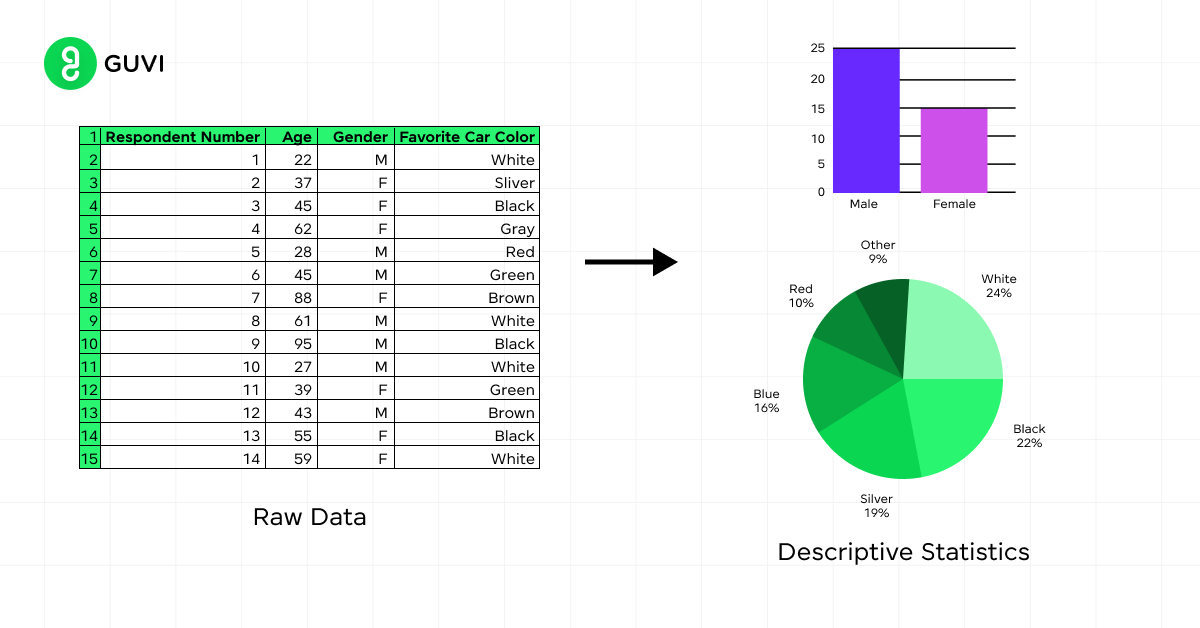
When you use descriptive statistics, you’re not making generalizations or inferences about a larger population. Instead, you’re focusing on describing and analyzing the data you have at hand.
Key Components
To get a comprehensive view of your data, descriptive statistics employs several key components:
- Measures of Central Tendency: These include the mean, median, and mode, which give you an idea of the average or typical value in your dataset.
- Measures of Variability: These show how spread out your data is and include the range, variance, and standard deviation.
- Distribution Shape: This looks at aspects like skewness and kurtosis to understand how your data is distributed.
- Graphical Representations: Charts, graphs, and tables help you visualize your data. Common types include histograms, bar charts, pie charts, scatter plots, and box plots.
Importance in Data Analysis
Descriptive statistics plays a crucial role in data analysis by:
- Providing basic information about variables in your dataset
- Highlighting potential relationships between variables
- Giving you a clear picture of what your current data shows
It’s important to note that descriptive statistics only make statements about the dataset you’re analyzing. They don’t go beyond your data or make projections. However, they do provide a solid foundation for further statistical analysis and decision-making processes.
By using descriptive statistics, you can effectively summarize and communicate the key characteristics of your dataset, making it easier to understand patterns, trends, and distributions within your data.
Types of Descriptive Statistics
Descriptive statistics allow you to characterize your data based on its properties. There are four major types of descriptive statistics that help you summarize and interpret numerical information effectively.
A) Frequency Distribution
A frequency distribution describes the number of observations for each possible value of a variable. It’s the most primitive way (the most basic hence, this is all we’ll discuss about it in this article) to present a distribution, typically listing values from lowest to highest.
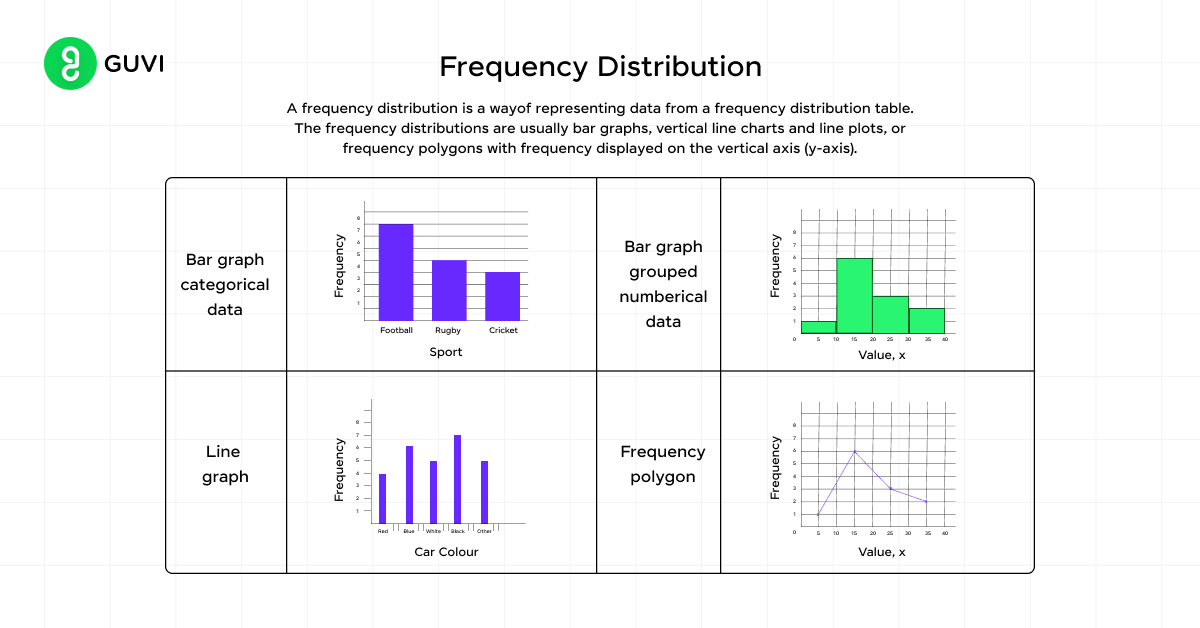
You can display frequency distributions using:
- Frequency tables: Two-column tables showing values and their frequencies
- Graphs: Pie charts, bar charts, and histograms
There are four types of frequency distributions:
- Ungrouped frequency distributions
- Grouped frequency distributions
- Relative frequency distributions
- Cumulative frequency distributions
B) Central Tendency
Measures of central tendency help you find the middle or average of a dataset. The three most common measures are:
- Mode: The most frequent value in a dataset
- Median: The middle number in an ordered dataset
- Mean: The sum of all values divided by the total number of values
These measures attempt to describe what a typical data point might look like. The mean is the most commonly used measure of central tendency.
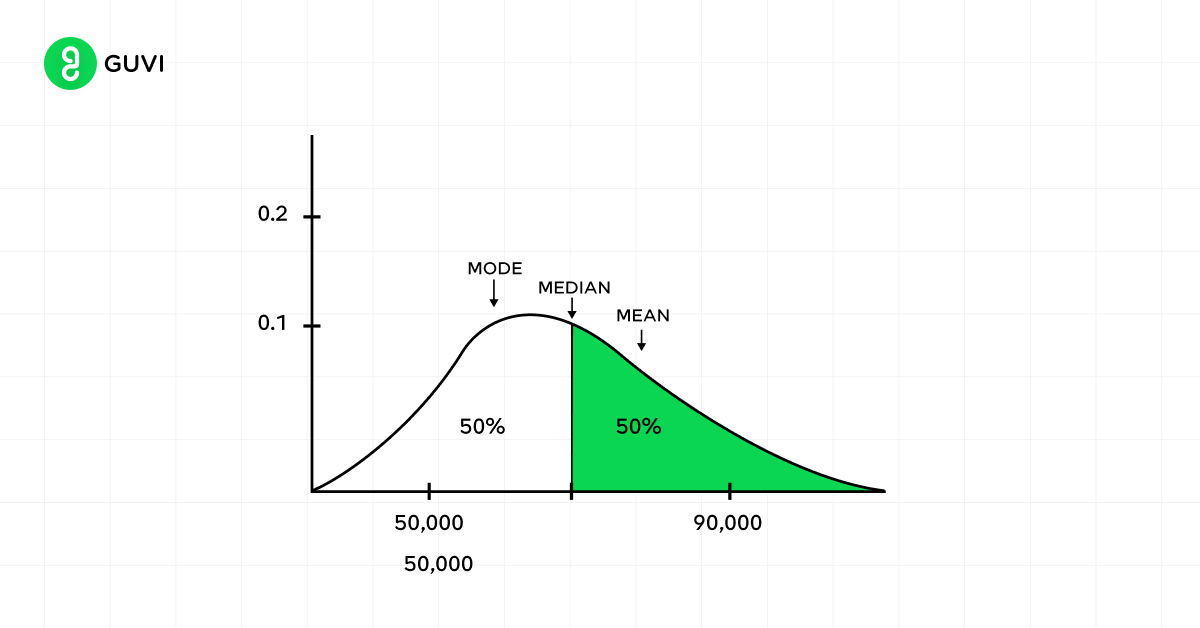
Measures of Central Tendency
When you’re analyzing data, understanding the center of your distribution is crucial. Measures of central tendency help you pinpoint the typical or representative values in your dataset. Let’s explore the three main measures: mean, median, and mode.
1. Mean
The mean, often referred to as the average, is the sum of all observations divided by the total number of observations. It’s represented by the formula:
x̄ = (1/n) * Σ(xi)
Where n is the number of observations and xi represents each individual value.
For example, if you have salaries of ₹50,000, ₹55,000, and ₹60,000, the mean would be:
(₹50,000 + ₹55,000 + ₹60,000) / 3 = ₹55,000
The mean is sensitive to extreme values, which can skew your results. In such cases, you might consider using a trimmed mean, which removes a certain percentage of the highest and lowest values before calculating.
2. Median
The median is the middle value when your data is arranged in order. To find it:
- Sort your data from lowest to highest.
- For an odd number of observations, select the middle number.
- For an even number, take the average of the two middle numbers.
The median is less affected by outliers than the mean, making it useful for skewed distributions. For instance, in income data, extremely high earners can significantly pull up the mean, while the median gives a better representation of a typical income.
3. Mode
The mode is the value that appears most frequently in your dataset. A distribution can have one mode (unimodal), two modes (bimodal), or multiple modes (multimodal). Some datasets may not have a mode at all.
For example, in the set {2, 3, 3, 4, 5, 5, 5, 6}, the mode is 5.
The mode is particularly useful for categorical data where calculating a mean or median doesn’t make sense.
By using these measures of central tendency, you can gain valuable insights into the typical values of your data, helping you make more informed decisions in your statistical analysis.
C) Variability
Variability refers to the spread of scores in a distribution. It helps you understand how spread out your data is from the central tendency. Common measures of variability include:
- Range: The difference between the largest and smallest values
- Interquartile Range (IQR): The range of the middle 50% of scores
- Variance: The average squared difference of scores from the mean
- Standard Deviation: The average amount by which scores differ from the mean
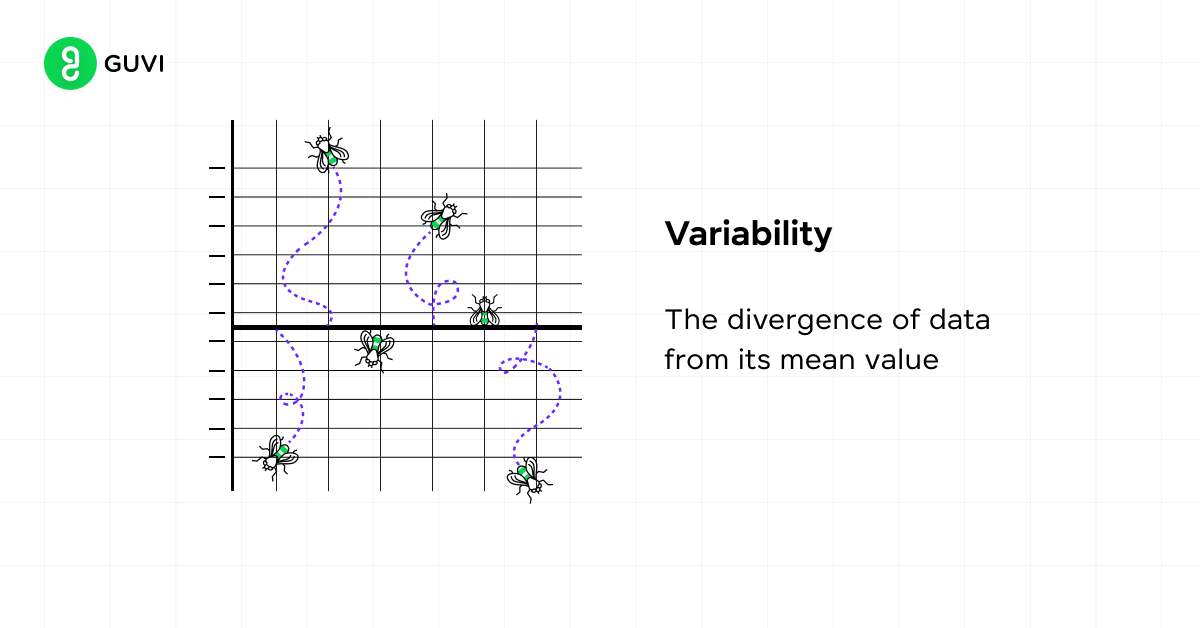
These measures provide insights into the dispersion of your data, helping you make more informed decisions based on your dataset’s characteristics. Now let us discuss the measures of central tendency and variability in detail.
Before we move into the next section, ensure you have a good grip on data science essentials like Python, MongoDB, Pandas, NumPy, Tableau & PowerBI Data Methods. If you are looking for a detailed course on Data Science, you can join GUVI’s Data Science Course with Placement Assistance. You’ll also learn about the trending tools and technologies and work on some real-time projects.
Additionally, if you want to explore Python through a self-paced course, try GUVI’s Python Certification course.
Measures of Variability
When you’re analyzing data, understanding how spread out your values are is just as important as knowing their central tendency. Measures of variability help you quantify this spread, giving you a clearer picture of your dataset’s distribution.
Let’s explore four key measures of variability: range, variance, standard deviation, and interquartile range.
1. Range
The range is the simplest measure of variability, calculated by subtracting the lowest value from the highest value in your dataset. It gives you a quick idea of how spread out your data is.
For example, if you have a dataset of exam scores ranging from 65 to 98, the range would be 33 points. While easy to calculate, the range has limitations. It’s sensitive to outliers and doesn’t tell you much about how the data is distributed between the extremes.
2. Variance
Variance digs deeper into your data’s spread. It measures how far each number in the set is from the mean. The formula for variance is:
σ² = Σ(x – μ)² / N
Where σ² is the variance, x represents each value in the dataset, μ is the mean, and N is the number of values. A larger variance indicates that your data points are further from the mean and from each other.
While variance provides valuable information, its squared units can make interpretation challenging.
3. Standard Deviation
To address the interpretation issue of variance, you can use standard deviation. It’s simply the square root of the variance, bringing the measure back to your original units. The formula is:
σ = √(Σ(x – μ)² / N)
Standard deviation tells you, on average, how far each value is from the mean.
For example, if the mean height in a group is 170 cm with a standard deviation of 5 cm, you know that most heights fall within 5 cm above or below 170 cm. This measure is widely used in statistics and provides a reliable indicator of spread.
4. Interquartile Range (IQR)
The interquartile range focuses on the middle 50% of your data, making it resistant to outliers. To calculate the IQR, you first need to find the first quartile (Q1, 25th percentile) and the third quartile (Q3, 75th percentile). The IQR is then calculated as:
IQR = Q3 – Q1
This measure is particularly useful for skewed distributions where the mean and standard deviation might be misleading. It’s often used in box plots to visualize data spread.
By using these measures of variability, you can gain a comprehensive understanding of how your data is distributed, helping you make more informed decisions in your statistical analysis.
Univariate vs. Bivariate
Univariate Analysis
When you’re dealing with descriptive statistics, univariate analysis is the simplest form you’ll encounter. It involves examining a single variable at a time. This approach allows you to summarize and describe the distribution of that variable without considering relationships with other factors.
In univariate analysis, you focus on measures such as:
- Central tendency (mean, median, mode)
- Dispersion (range, standard deviation, variance)
- Distribution shape (skewness, kurtosis)
To visualize univariate data, you can use tools like histograms, box plots, or violin plots. These graphical representations help you understand the spread of your data and identify potential outliers.
Bivariate Analysis
Bivariate analysis takes your statistical exploration a step further by examining the relationship between two variables. This approach allows you to understand how changes in one variable might correspond to changes in another.
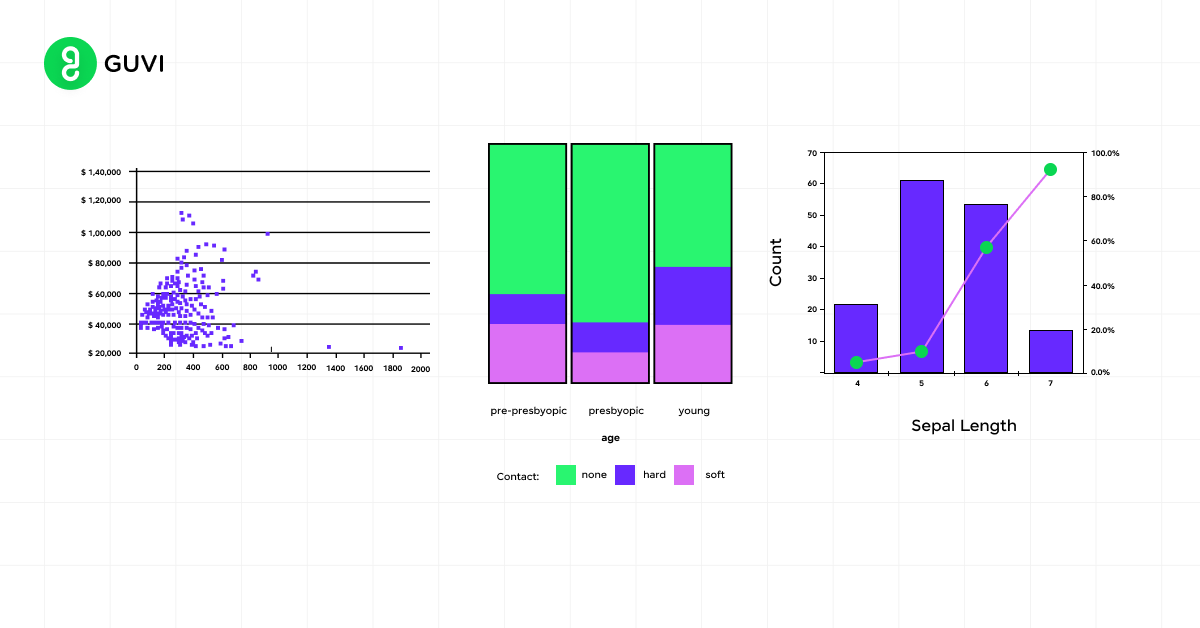
Key aspects of bivariate analysis include:
- Identifying relationships (positive, negative, or no clear pattern)
- Measuring correlation strength
- Visualizing data using scatter plots
The correlation coefficient, ranging from -1 to 1, quantifies the strength and direction of the linear relationship between your two variables.
Comparing the Two Approaches
To better understand the differences between univariate and bivariate analysis, consider this comparison:
| Aspect | Univariate | Bivariate |
| Variables | One | Two |
| Focus | Distribution and summary of a single variable | Relationship between two variables |
| Common visualizations | Histograms, box plots | Scatter plots, regression plots |
| Key statistics | Mean, median, mode, standard deviation | Correlation coefficient |
| Hypothesis testing | Simple hypotheses about a single variable | Hypotheses about associations between variables |
By using both univariate and bivariate analyses, you gain a comprehensive understanding of your data, from individual variable characteristics to potential relationships between variables. Learn more through data analytics projects.
Visualizing Descriptive Statistics
When you’re working with descriptive statistics, visualizing your data can provide valuable insights. Let’s explore four powerful tools to help you understand and present your data effectively.
1. Histograms
Histograms are excellent for displaying the distribution of continuous data. To create a histogram in Excel, select your data and use the histogram option in the chart menu. This graph allows you to observe the frequency of values within specific ranges.
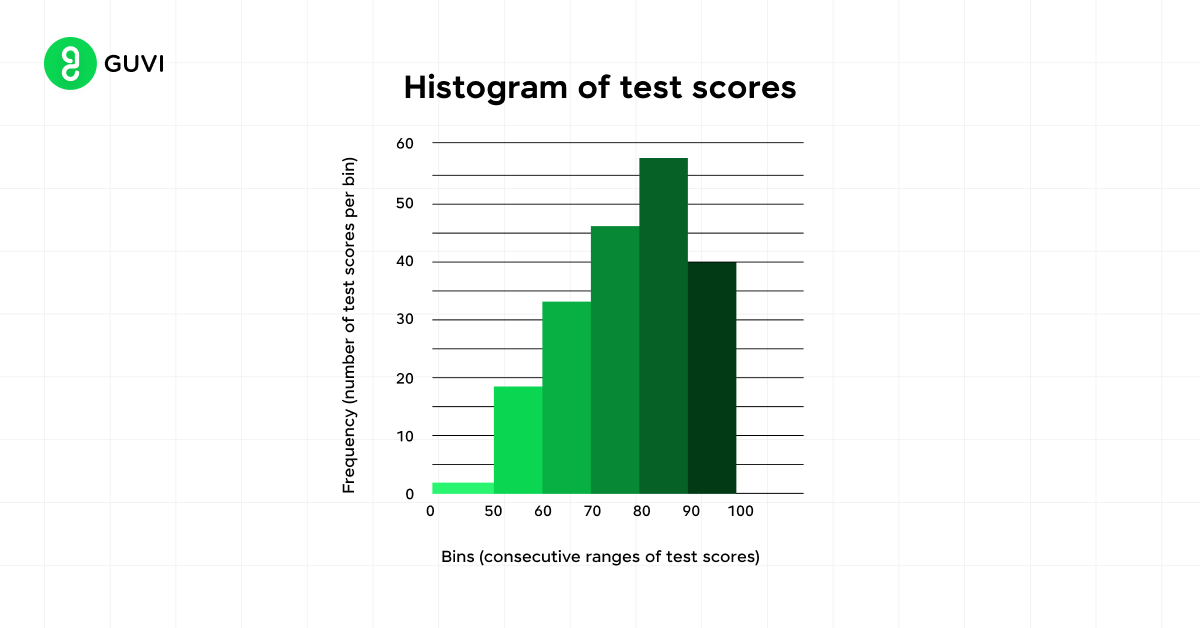
Key features of histograms include:
- Central location: Represented by mean, median, and mode
- Spread: Illustrated by the range and standard deviation
- Skewness: Measures the asymmetry of the distribution
- Kurtosis: Indicates the weight of the tails relative to the distribution’s center
2. Box Plots
Box plots, also known as box and whisker plots, provide a concise summary of your data’s distribution. They display the five-number summary: minimum, first quartile, median, third quartile, and maximum.
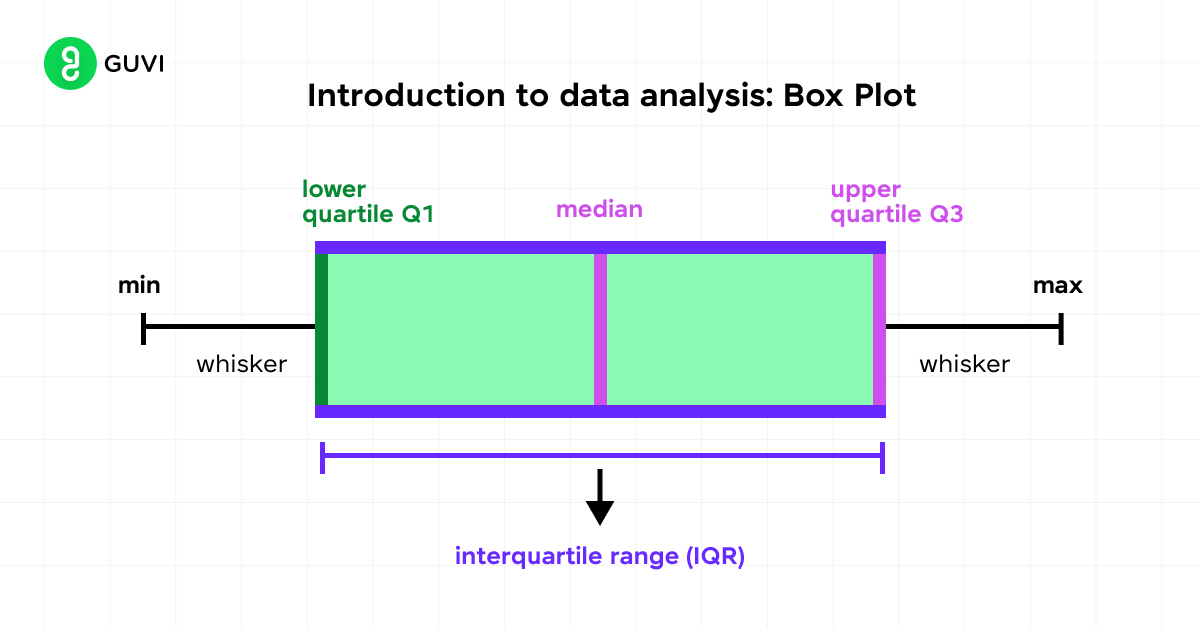
To interpret a box plot:
- The box represents the interquartile range (IQR)
- The line inside the box shows the median
- Whiskers extend to the minimum and maximum values
- Outliers are plotted as individual points beyond the whiskers
Box plots are particularly useful for comparing distributions across different groups or samples.
3. Scatter Plots
Scatter plots help you visualize relationships between two continuous variables. Each point on the graph represents an individual data point, with one variable on the x-axis and the other on the y-axis.
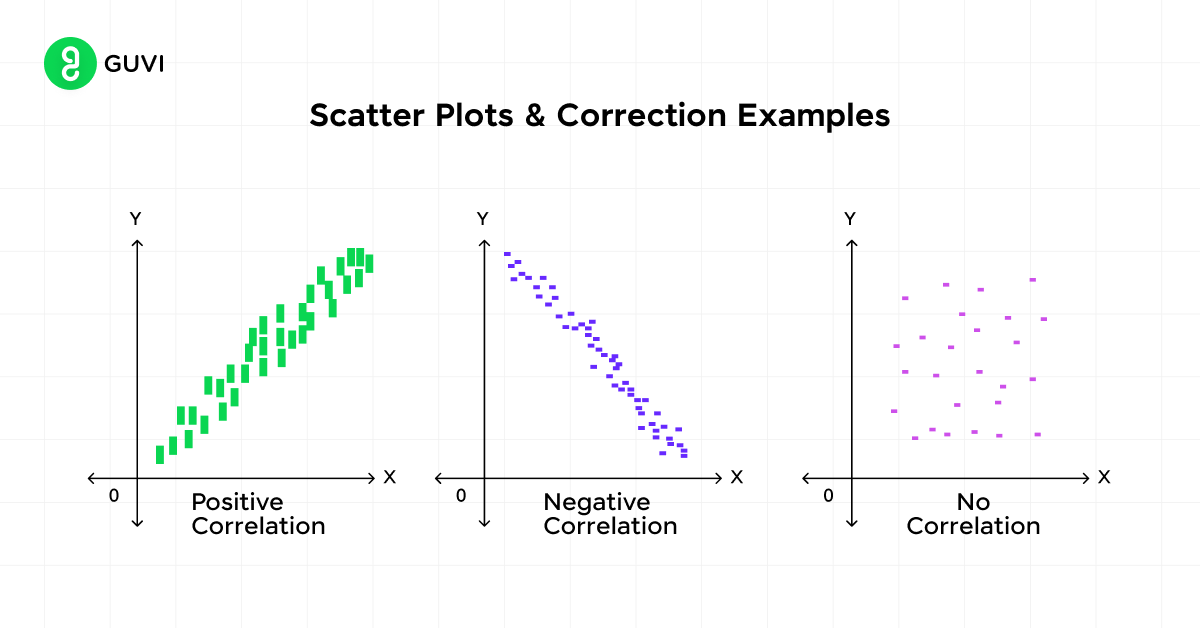
Key aspects to observe in scatter plots:
- Direction: Positive or negative relationship
- Form: Linear or curved relationship
- Strength: How closely the points cluster together
4. Bar Charts
Bar charts are ideal for displaying categorical data. They use rectangular bars to represent the frequency or proportion of each category.
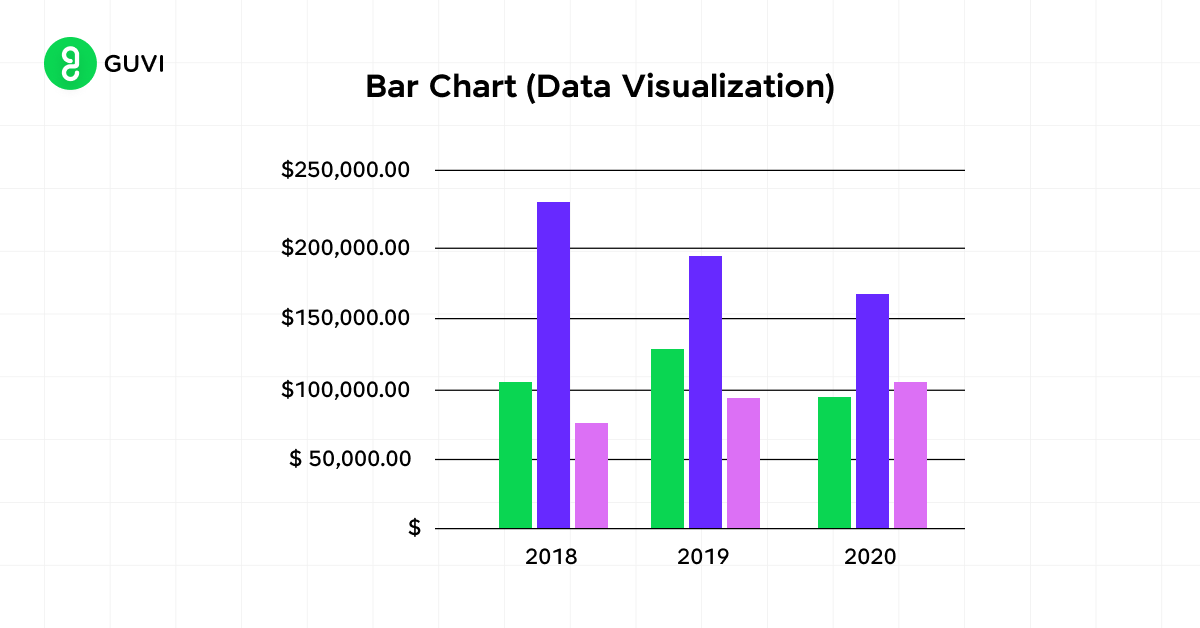
When creating bar charts:
- Ensure all bars start at a zero baseline
- Consider sorting bars from longest to shortest for easier comparison
- Use color purposefully to highlight specific categories or groups
By utilizing these visualization techniques, you can gain deeper insights into your data’s characteristics and effectively communicate your findings.
Applications of Descriptive Statistics
Descriptive statistics play a crucial role in various fields, helping you make sense of complex data and draw meaningful insights. Let’s explore how these powerful tools are applied in different sectors.
1. Business and Finance
In the world of business and finance, descriptive statistics are invaluable for decision-making. You can use them to:
- Analyze financial information to make informed decisions
- Monitor relationships between variables using scatter plots
- Summarize and communicate key characteristics of financial datasets
For instance, when examining stock returns, you might calculate the average annual return, standard deviation, and median. This allows you to compare different asset classes and understand their risk-return profiles. Here’s an example using data from 1928 to 2020:
| Asset Class | Average Annual Return | Standard Deviation | Median Return |
| U.S. Stocks | 11.64% | 19.49% | 14.22% |
| 10-Year Treasury Bonds | 5.21% | Lower than stocks | Lower than average |
| T-Bills | 3.36% | Lowest | Lower than average |
2. Healthcare and Medicine
In healthcare and medicine, descriptive statistics help you:
- Summarize patient data
- Analyze test scores and survey results
- Present findings visually using histograms, pie charts, and scatter plots
For example, you might use descriptive statistics to examine the distribution of patient ages in a study or to analyze the effectiveness of a new treatment by comparing mean outcomes between groups.
3. Education
Educators rely on descriptive statistics to:
- Make sense of test scores and performance data
- Identify areas where students excel or struggle
- Tailor educational strategies to meet learners’ needs
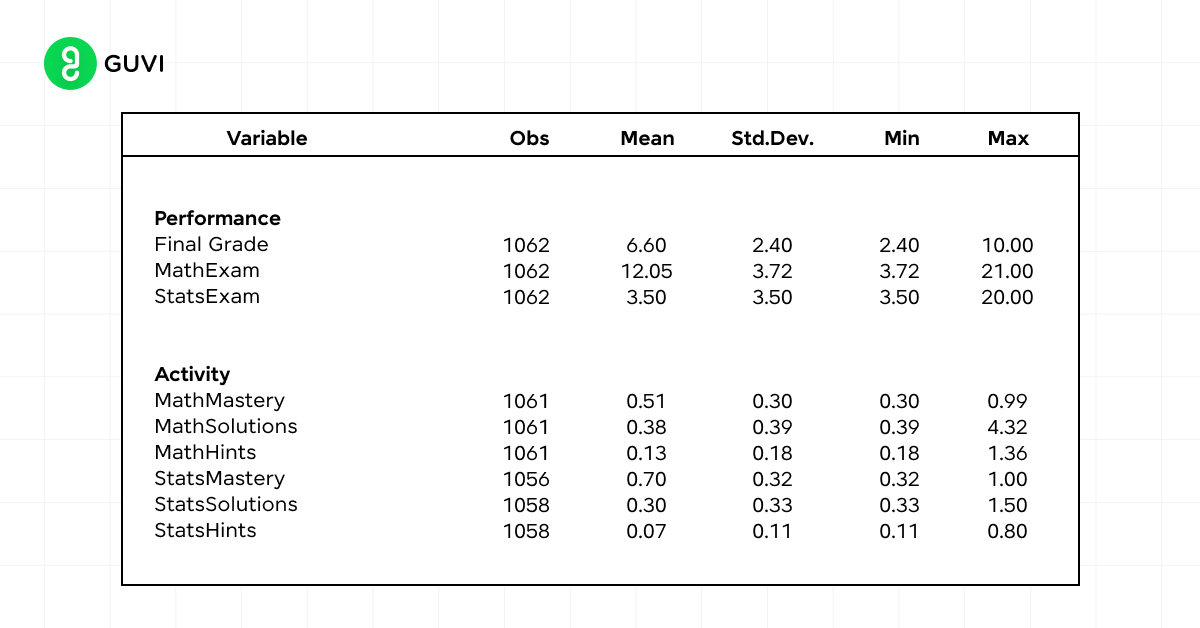
You can use measures of central tendency (mean, median, mode) to understand average student performance, and measures of variability (range, standard deviation) to assess the consistency of scores across a class.
4. Social Sciences
In social sciences, descriptive statistics help you:
- Summarize survey results
- Analyze demographic data
- Identify patterns and trends in social phenomena
For instance, you might use frequency distributions to examine the age distribution in a population study or calculate percentiles to understand income distribution in a socioeconomic analysis.
By applying descriptive statistics across these fields, you can transform raw data into meaningful information, enabling better decision-making and deeper insights into complex phenomena.
Kickstart your Data Science journey by enrolling in GUVI’s Data Science Course where you will master technologies like MongoDB, Tableau, PowerBI, Pandas, etc., and build interesting real-life projects.
Alternatively, if you want to explore Python through a self-paced course, try GUVI’s Python Certification course.
Concluding Thoughts…
Descriptive statistics serve as a powerful tool to analyze and interpret data across various fields. From business and finance to healthcare and education, these methods provide valuable insights into complex datasets.
By learning about its key characteristics, identifying patterns, and presenting information visually, descriptive statistics enable better decision-making and a deeper understanding of data.
As you start your data analysis journey, remember that descriptive statistics form the foundation for more advanced statistical techniques. They offer a clear picture of your data’s main features, helping you to spot trends and formulate hypotheses.
FAQs
What is descriptive statistics and its types?
Descriptive statistics summarize and organize data in a meaningful way. Types include measures of central tendency (mean, median, mode), measures of variability (range, variance, standard deviation), and measures of frequency (count, frequency distribution).
What is the overview of statistics?
Statistics is the science of collecting, analyzing, interpreting, and presenting data. It includes descriptive statistics for summarizing data and inferential statistics for making predictions or inferences about a population based on sample data.
What is the main purpose of descriptive statistics?
The main purpose of descriptive statistics is to provide a simple summary of the data, making it easier to understand and interpret large amounts of information by highlighting patterns and trends.
Who is the father of statistics?
Sir Ronald A. Fisher is often referred to as the father of modern statistics for his contributions to experimental design and statistical inference.






















Did you enjoy this article?