
RSA vs DSA: Understanding the Core Differences
Nov 26, 2025 8 Min Read 940 Views
(Last Updated)
How does a system know that a digital message truly came from its claimed source? The answer is in cryptographic algorithms like RSA and DSA. They protect the integrity and confidentiality of data exchanged over digital networks. Both algorithms rely on complex mathematical principles but serve distinct purposes. Understanding how these two systems differ helps security professionals and developers choose the right algorithm for their specific needs in online communication and data validation.
Read the full blog to explore how RSA and DSA function and their key benefits. Also, explore technical mechanisms, Python implementations, and practical applications across digital systems. Let’s learn more:
Table of contents
- What is RSA?
- What is DSA?
- Benefits of RSA vs. DSA
- Advantages of RSA
- Advantages of DSA
- Top Applications of RSA vs. DSA
- Applications of RSA
- Applications of DSA
- Working Mechanism of RSA
- Step 1: Selection of Prime Numbers
- Step 2: Calculation of the Modulus
- Step 3: Determination of Euler’s Totient
- Step 4: Selection of the Public Key Exponent
- Step 5: Computation of the Private Key Exponent
- Step 6: Formation of Key Pairs
- Step 7: Encryption Process
- Step 8: Decryption Process
- Step 9: Verification and Authentication
- Working Mechanism of DSA
- Step 1: Parameter Generation
- Step 2: Computation of the Generator
- Step 3: Private and Public Key Generation
- Step 4: Message Hashing
- Step 5: Signature Generation
- Step 6: Signature Transmission
- Step 7: Verification Preparation
- Step 8: Signature Verification
- Step 9: Integrity and Authentication Assurance
- RSA Algorithm Implementation in Python
- DSA Implementation in Python (using cryptography)
- Limitations of RSA
- Limitations of DSA
- Comparison Table: RSA and DSA Algorithms
- Quick Quiz: RSA vs DSA
- Conclusion
- FAQs
- Which algorithm is better for encryption, RSA or DSA?
- Can RSA and DSA be used together in a security system?
- Why is DSA preferred for digital signatures in government systems?
What is RSA?
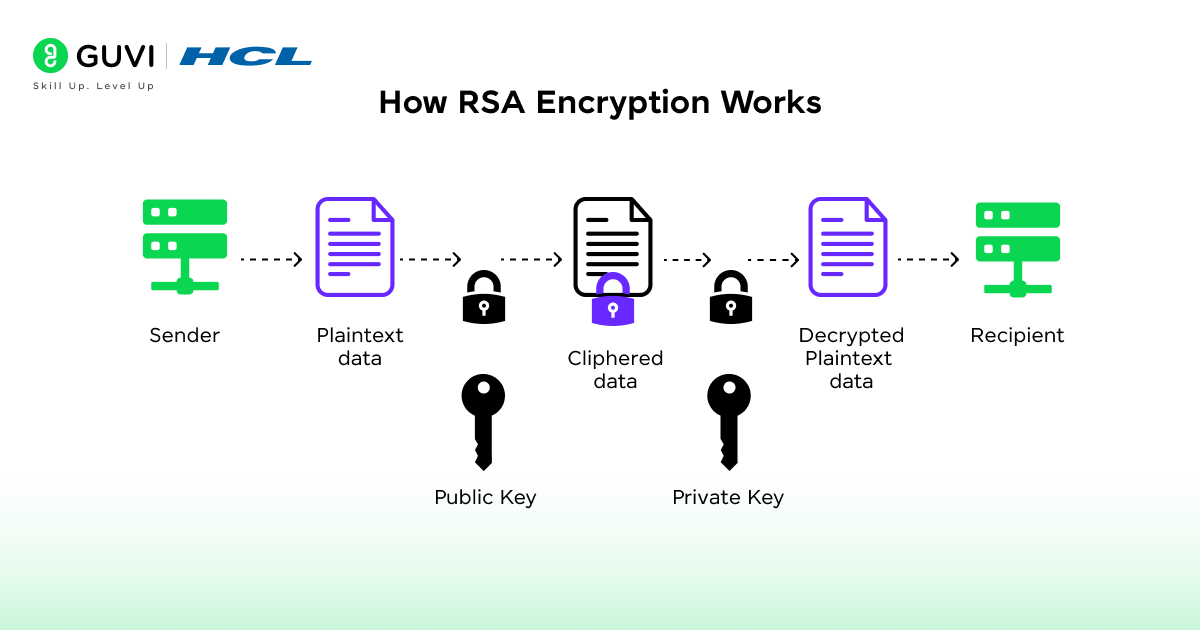
RSA is a cryptographic algorithm that secures digital communication through mathematical principles of prime factorization. It was introduced by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977 and remains one of the most trusted encryption systems in modern computing. The algorithm uses a pair of keys: one public and one private to encrypt and decrypt information. It creates a secure channel between parties who may have never interacted before. The reliability of RSA is in the strength of these numbers and the precision of the algorithm’s mathematical structure. It is widely used in online transactions and data protection systems that require confidentiality and authenticity.
What is DSA?
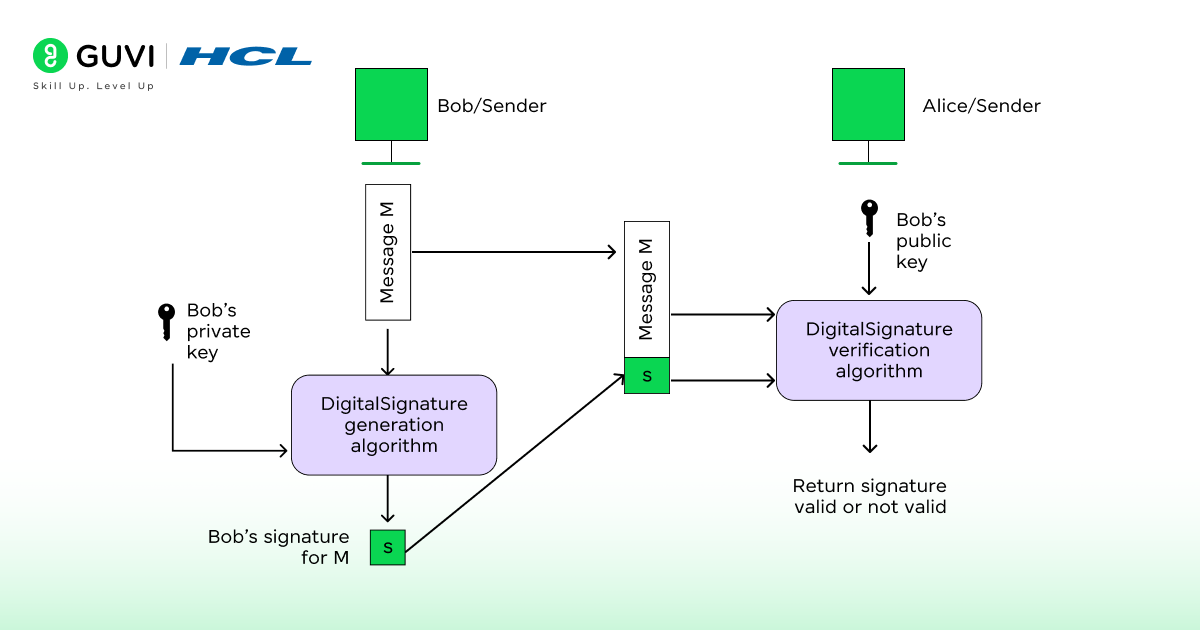
The Digital Signature Algorithm, known as DSA, is a cryptographic standard that authenticates digital information through mathematical precision. It was introduced by the National Institute of Standards and Technology in 1991 as part of the Digital Signature Standard. The core purpose of DSA is to validate the integrity and origin of electronic documents or software. It does not encrypt the message itself but guarantees that any modification in the content can be detected immediately. The system depends on modular arithmetic and the discrete logarithm problem, which makes it resistant to unauthorized tampering.
Benefits of RSA vs. DSA
Advantages of RSA

- Strong Security
RSA provides robust protection for digital communication through its reliance on complex mathematical principles. The use of large prime numbers makes decryption without the private key almost impossible. This structure creates a high level of trust in online transactions and data exchanges.
- Data Integrity
The algorithm supports digital signatures that confirm data authenticity. It guarantees that a message or document remains unchanged during transmission. Any alteration becomes easily detectable, which reinforces verification processes.
- Authentication
RSA helps in verifying the identity of users and systems. The private and public key pair allows organizations to confirm that data originates from a legitimate source. This procedure prevents impersonation and unauthorized access.
- Compatibility with Modern Systems
RSA works efficiently with various encryption protocols and software applications. Its adaptability supports secure communication in different technological environments such as web browsers and secure email platforms.
Advantages of DSA

- Strong Authentication
DSA provides a reliable mechanism for verifying the identity of the sender. The digital signature produced through private key operations confirms that the message originates from a legitimate source. This prevents impersonation and maintains trust in communication.
- Data Integrity
Any alteration in the original message leads to a mismatch during the verification process. This property ensures that the transmitted information remains unmodified. The usage of hashing functions adds another layer of protection against data corruption.
- Regulatory Acceptance
DSA has received global acceptance as a part of international cryptographic standards. Its recognition in legal and financial frameworks increases confidence in electronic transactions. Many digital governance systems prefer DSA for its compliance with established security regulations.
- Efficient Verification Process
The verification phase in DSA consumes fewer computational resources than many other public-key systems. This efficiency supports large-scale applications such as document authentication and digital record validation.
- Separation of Encryption and Authentication
DSA focuses exclusively on authentication rather than combining it with encryption. This separation reduces computational overhead and simplifies security architecture in systems that already employ other encryption techniques.
Top Applications of RSA vs. DSA
Applications of RSA

- Secure Web Communication
RSA plays a vital role in establishing secure connections on the internet. Protocols like HTTPS rely on RSA to protect sensitive data transferred between users and websites. It safeguards login credentials and personal information.
- Digital Signatures
Organizations use RSA to create and verify digital signatures on documents. This practice confirms the sender’s identity and confirms that the file remains untampered. It is widely used in legal and governmental systems.
- Email Encryption
RSA protects email content from unauthorized reading. It encrypts the message using the recipient’s public key, which keeps confidential communication private. Only the intended receiver with the correct private key can access the original message.
- Secure Software Distribution
Software developers apply RSA to verify the authenticity of distributed applications. Digital certificates signed with RSA keys confirm that the software originates from a trusted source. This prevents malware disguised as legitimate programs from spreading.
- Virtual Private Networks (VPNs)
RSA supports secure VPN connections by managing key exchanges and authentication. It helps establish encrypted tunnels for data transfer, which levels up privacy and protects user activity on public networks.
Applications of DSA

- Digital Certificates
DSA plays a vital role in the generation and validation of digital certificates used in secure communications. Certificate authorities apply DSA to sign certificates that confirm the authenticity of websites, software, and network entities.
- Secure Software Distribution
Software vendors use DSA to sign executable files and updates. The signature confirms that the software originates from a trusted developer and that it has not been altered. This helps protect systems against malicious downloads.
- E-Governance Systems
Government platforms use DSA to validate digital forms, legal records, and identification systems. The algorithm bolsters document verification processes and supports electronic workflow transparency.
- Financial Transactions
Electronic payment platforms use DSA-based digital signatures to validate transaction data. It prevents unauthorized modifications and makes sure that records remain accurate across financial networks.
- Document Management and Legal Communication
Organizations apply DSA to authenticate digital contracts and correspondence. The verifiable nature of DSA signatures augments trust between parties and provides a legal basis for electronic approvals.
Working Mechanism of RSA
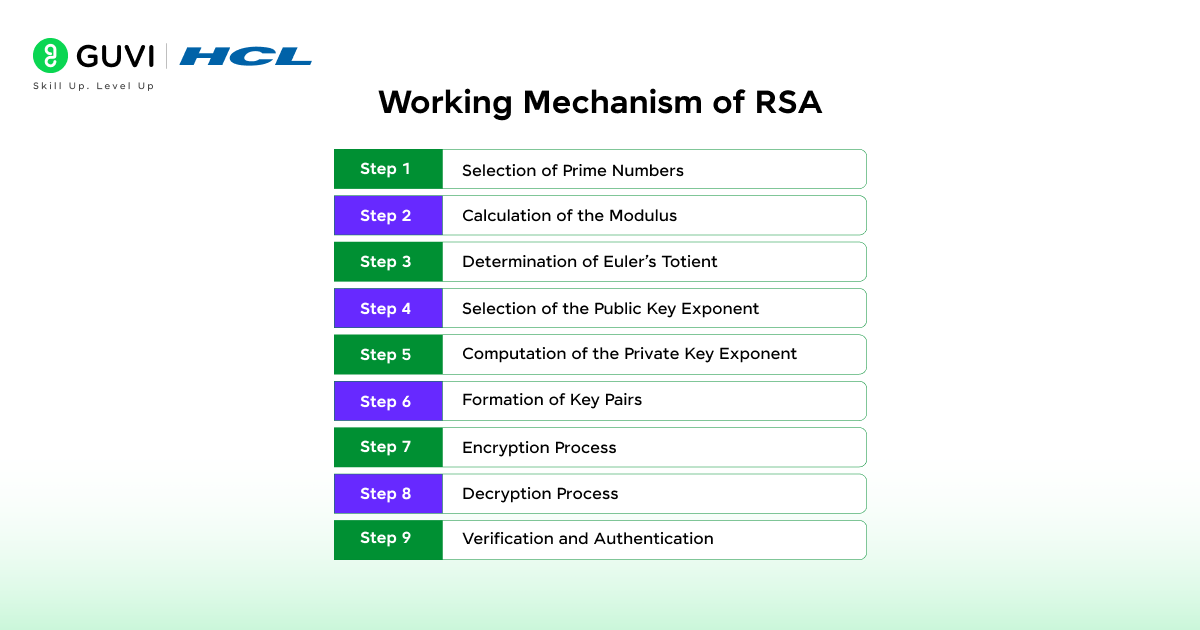
Step 1: Selection of Prime Numbers
The process begins with the selection of two large prime numbers, usually denoted as p and q. These numbers must be random and distinct to prevent any prediction or repetition. Their product forms the base for the encryption system, which becomes a part of the public and private keys.
Step 2: Calculation of the Modulus
The chosen primes are multiplied to produce n = p × q. This modulus n defines the numerical range of the cryptographic system. Both the public and private keys use n, and its size directly affects the security strength of the algorithm.
Step 3: Determination of Euler’s Totient
Euler’s Totient function is computed as φ(n) = (p − 1)(q − 1). This value represents the count of integers less than n that are relatively prime to it. It plays a critical role in the construction of the keys, as it influences both encryption and decryption exponents.
Step 4: Selection of the Public Key Exponent
A number e is chosen such that it is greater than one and less than φ(n). It must also be coprime with φ(n), meaning it shares no common factors other than one. The value of e becomes the public key exponent used for encrypting messages.
Step 5: Computation of the Private Key Exponent
The private key exponent d is calculated as the modular inverse of e under φ(n). This means that (d × e) mod φ(n) = 1. The value of d remains confidential and is essential for decrypting encrypted data accurately.
Step 6: Formation of Key Pairs
The public key consists of (e, n), and the private key consists of (d, n). The public key is shared openly for encryption processes, whereas the private key remains with the owner. Both are mathematically related, yet it is computationally infeasible to determine d from e and n.
Step 7: Encryption Process
The sender converts the plaintext message into a numerical format less than n. The ciphertext is produced using the formula C = M^e mod n, where M represents the message. The result is a coded message that can be safely transmitted.
Step 8: Decryption Process
The receiver uses the private key to retrieve the original message. The formula M = C^d mod n is applied to the ciphertext. The process restores the plaintext message without loss of information.
Step 9: Verification and Authentication
RSA also supports digital signatures to confirm data authenticity. The sender signs a hash of the message using the private key. The receiver verifies it using the sender’s public key, which assures both integrity and origin of the data.
Each step works in mathematical harmony to create a secure communication channel. The precision of key generation and the computational complexity of prime factorization make RSA a trusted standard in cryptography.
Working Mechanism of DSA
Step 1: Parameter Generation
The Digital Signature Algorithm begins with the generation of specific mathematical parameters. A large prime number is selected to define the finite field used in computations. Another prime number q is chosen such that q divides p − 1. These values provide the mathematical foundation for the digital signature process.
Step 2: Computation of the Generator
A value g is computed using the formula g = h^{(p−1)/q} mod p, where h is an integer less than p − 1. The chosen h must produce a g greater than one. The generator g becomes a public parameter that supports the modular arithmetic used in signing and verification.
Step 3: Private and Public Key Generation
The user selects a random integer x such that 0 < x < q. This value serves as the private key and must remain secret. The public key y is then computed as y = g^x mod p. Both keys are mathematically related through exponentiation, yet deriving x from y remains computationally infeasible due to the discrete logarithm problem.
Step 4: Message Hashing
The original message is processed through a cryptographic hash function to generate a fixed-size digest. This digest represents the message in a condensed format and prevents direct exposure of the original content. Any change in the message produces a completely different hash, which helps maintain data integrity.
Step 5: Signature Generation
A random integer k is chosen such that 0 < k < q. The value of k must remain unique for every signature to prevent private key exposure. The first part of the signature, r, is computed as (g^k mod p) mod q. The second part, s, is computed as (k^{-1}(H(M) + x × r)) mod q, where H(M) represents the hash of the message. The pair (r, s) forms the complete digital signature that accompanies the message.
Step 6: Signature Transmission
The sender transmits the message along with its signature to the recipient. The message can be sent in plain or encrypted form, depending on the communication protocol. The recipient uses the public parameters to verify the authenticity of the received data.
Step 7: Verification Preparation
The verifier computes the hash of the received message to obtain H(M). Then, two intermediate values are calculated. The first is w = s^{-1} mod q, which represents the modular inverse of s. The second is u₁ = (H(M) × w) mod q and u₂ = (r × w) mod q. These values prepare the ground for signature validation.
Step 8: Signature Verification
A verification variable v is calculated as ((g^{u₁} × y^{u₂}) mod p) mod q. The signature is accepted as valid only if v = r. This comparison confirms that the message originated from the correct private key holder and that the content has not been altered during transmission.
Step 9: Integrity and Authentication Assurance
The process concludes with the assurance of both integrity and authenticity. The digital signature validates the origin of the message and confirms that the data remains intact. Any modification leads to verification failure, which maintains the reliability of communication systems using DSA.
The steps of DSA work through precise modular arithmetic and secure key relationships. Each component contributes to a system that protects digital information through mathematical verification rather than secrecy of the transmission channel.
RSA Algorithm Implementation in Python
import random
from math import gcd
# Step 1: Function to generate a random prime number
def generate_prime_candidate(length):
"""Generate an odd integer randomly within a given bit length."""
p = random.getrandbits(length)
p |= (1 << length - 1) | 1 # Ensure MSB and LSB are set to make it odd and of correct length
return p
def is_prime(n, k=10):
"""Miller-Rabin primality test for checking if n is prime."""
if n <= 3:
return n == 2 or n == 3
if n % 2 == 0:
return False
# Write n−1 as 2^r * d
r, d = 0, n - 1
while d % 2 == 0:
r += 1
d //= 2
# Perform k rounds of testing
for _ in range(k):
a = random.randrange(2, n - 1)
x = pow(a, d, n)
if x == 1 or x == n - 1:
continue
for _ in range(r - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
def generate_prime_number(length=512):
"""Generate a prime number of specified bit length."""
p = 4
while not is_prime(p):
p = generate_prime_candidate(length)
return p
# Step 2: Key generation
def generate_keys(keysize=512):
p = generate_prime_number(keysize)
q = generate_prime_number(keysize)
n = p * q
phi = (p - 1) * (q - 1)
# Choose e such that 1 < e < phi and gcd(e, phi) = 1
e = 65537 # Commonly used prime exponent
if gcd(e, phi) != 1:
e = 3
while gcd(e, phi) != 1:
e += 2
# Compute modular inverse of e
d = pow(e, -1, phi)
public_key = (e, n)
private_key = (d, n)
return public_key, private_key
# Step 3: Encryption and Decryption
def encrypt(message, public_key):
e, n = public_key
message_int = int.from_bytes(message.encode('utf-8'), byteorder='big')
cipher_int = pow(message_int, e, n)
return cipher_int
def decrypt(cipher_int, private_key):
d, n = private_key
message_int = pow(cipher_int, d, n)
message_bytes = message_int.to_bytes((message_int.bit_length() + 7) // 8, byteorder='big')
return message_bytes.decode('utf-8')
# Step 4: Demonstration
if __name__ == "__main__":
public_key, private_key = generate_keys(512)
print("Public Key:", public_key)
print("Private Key:", private_key)
message = "RSA algorithm in Python"
print("\nOriginal Message:", message)
cipher = encrypt(message, public_key)
print("Encrypted Message:", cipher)
decrypted = decrypt(cipher, private_key)
print("Decrypted Message:", decrypted)
Also, Read: Navigating the Best Datasets for Your Data Science Projects [2025]
DSA Implementation in Python (using cryptography)
from cryptography.hazmat.primitives.asymmetric import dsa
from cryptography.hazmat.primitives import hashes, serialization
from cryptography.exceptions import InvalidSignature
# Step 1: Generate DSA key pair
private_key = dsa.generate_private_key(key_size=2048)
public_key = private_key.public_key()
# Step 2: Message to be signed
message = b"Digital Signature Algorithm demonstration using cryptography library"
# Step 3: Sign the message using the private key
signature = private_key.sign(
message,
hashes.SHA256()
)
print("Digital Signature Generated Successfully.")
# Step 4: Verify the signature using the public key
try:
public_key.verify(
signature,
message,
hashes.SHA256()
)
print("Signature is valid. Message integrity and authenticity verified.")
except InvalidSignature:
print("Signature verification failed. The message or signature is invalid.")
# Step 5: Optional — Export keys for storage or transmission
# Export private key (PEM format)
private_pem = private_key.private_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PrivateFormat.PKCS8,
encryption_algorithm=serialization.NoEncryption()
)
# Export public key (PEM format)
public_pem = public_key.public_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PublicFormat.SubjectPublicKeyInfo
)
print("\nPrivate Key (PEM format):\n", private_pem.decode())
print("\nPublic Key (PEM format):\n", public_pem.decode())
Limitations of RSA
- Requires large key sizes to maintain strong security, which increases computational load.
- Encryption and decryption processes are slower compared to symmetric algorithms.
- Performance decreases with high-volume data encryption because RSA is suited for encrypting small blocks.
- Vulnerable to attacks if weak random number generators are used during key creation.
- Public key exposure can lead to security risks if key management practices are poor.
Limitations of DSA
- Signature generation speed is slower than RSA, especially for larger key sizes.
- Verification time can increase under high data loads.
- Depends heavily on the randomness of the value k; repetition or leakage of k compromises the private key.
- Provides authentication but does not support encryption, which limits its scope.
- Not suitable for systems requiring both encryption and signature operations through a single algorithm.
AI systems rely on the same logical and mathematical precision that drives algorithms like RSA and DSA. With our AI Software Development Course, you’ll master AI-driven programming, software integration, and model deployment, all while learning how structured algorithms shape intelligent systems. Build the expertise to design scalable, secure, and data-smart AI applications.
Comparison Table: RSA and DSA Algorithms
| Factor | RSA (Rivest–Shamir–Adleman) | DSA (Digital Signature Algorithm) |
| Primary Function | Used for both encryption and digital signatures | Used only for digital signatures and authentication |
| Mathematical Basis | Relies on the integer factorization problem | Based on the discrete logarithm problem |
| Introduced By | Ron Rivest, Adi Shamir, and Leonard Adleman in 1977 | National Institute of Standards and Technology (NIST) in 1991 |
| Key Type | Public and private key pair for encryption and decryption | Public and private key pair for signing and verification |
| Speed | Faster at signature generation but slower at verification | Faster at verification but slower at signature generation |
| Encryption Support | Supports encryption and decryption | Does not support encryption, only digital signatures |
| Performance | Requires larger key sizes for higher security | More efficient with smaller key sizes for the same security level |
| Security Dependency | Security depends on the difficulty of factoring large primes | Security depends on the complexity of solving discrete logarithms |
| Common Usage | HTTPS, VPNs, email encryption, and secure web communication | Digital certificates, government authentication, and financial validation |
| Standardization | Widely used in various public-key cryptosystems | Standardized under the Digital Signature Standard (DSS) |
| Key Weakness | Computationally heavy for large data encryption | Vulnerable if the random value k is reused or leaked |
| Best Suited For | Encrypted data transmission and digital verification | Digital signing, authentication, and data integrity verification |
Want to understand algorithms like RSA and DSA at their core? Build strong foundations in algorithms and problem-solving by enrolling in our Data Structures & Algorithms using Java Course. With hands-on Java code, real-life DSA challenges, and expert-led learning, you’ll level up your coding skills and prepare for technical interviews with confidence. Get started today!
Quick Quiz: RSA vs DSA
1. Who introduced the RSA algorithm?
a) Rivest, Shamir, and Adleman
b) Diffie and Hellman
c) ElGamal
d) NIST
2. What is the main purpose of the DSA algorithm?
a) Encrypting large datasets
b) Authenticating digital messages
c) Compressing data
d) Generating session keys
3. Which mathematical problem forms the basis of RSA?
a) Discrete logarithm problem
b) Integer factorization problem
c) Elliptic curve computation
d) Modular addition problem
4. Which algorithm is mainly used for digital signatures in government applications?
a) AES
b) RSA
c) DSA
d) Blowfish
5. What key pair does RSA use to secure communication?
a) Symmetric and private
b) Encryption and decryption
c) Public and private
d) Static and dynamic
Answer Key: 1-a, 2-b, 3-b, 4-c, 5-c
Conclusion
RSA and DSA both strengthen digital security through mathematical precision, yet they serve distinct goals. RSA excels in encryption and secure data exchange, while DSA focuses on authenticating digital messages and verifying integrity. Each algorithm plays a vital role in maintaining trust within modern communication systems. A balanced understanding of their mechanisms helps in choosing the right cryptographic approach for secure and authenticated digital interactions.
FAQs
1. Which algorithm is better for encryption, RSA or DSA?
RSA is better suited for encryption because it supports both encryption and digital signatures. DSA is mainly used for digital signatures and authentication but does not encrypt data.
2. Can RSA and DSA be used together in a security system?
Yes, RSA and DSA can work together. RSA can handle data encryption, and DSA can manage digital signatures, which strengthens all-around security.
3. Why is DSA preferred for digital signatures in government systems?
DSA is standardized under the Digital Signature Standard (DSS), which makes it reliable for government and regulatory applications requiring verified authenticity and data integrity.

























Did you enjoy this article?