A Guide on Linear Algebra for Data Science

Linear algebra is fundamental to data science, providing the mathematical foundation for understanding and manipulating data. With that being said, if you’re someone who has got no idea of how to use linear algebra in data science, you’ll learn and understand all here.

In this blog, we’re going to look into the concept of linear algebra for data science. It is indeed an important topic every data scientist must know. Not only the definition, but we’ll also talk about its importance and applications in the real-world. So, let’s get started:

What is Linear Algebra?

Linear algebra is a branch of mathematics that deals with vectors, vector spaces (or linear spaces), linear transformations, and systems of linear equations. It provides the theoretical underpinning for many areas of mathematics and applied sciences.

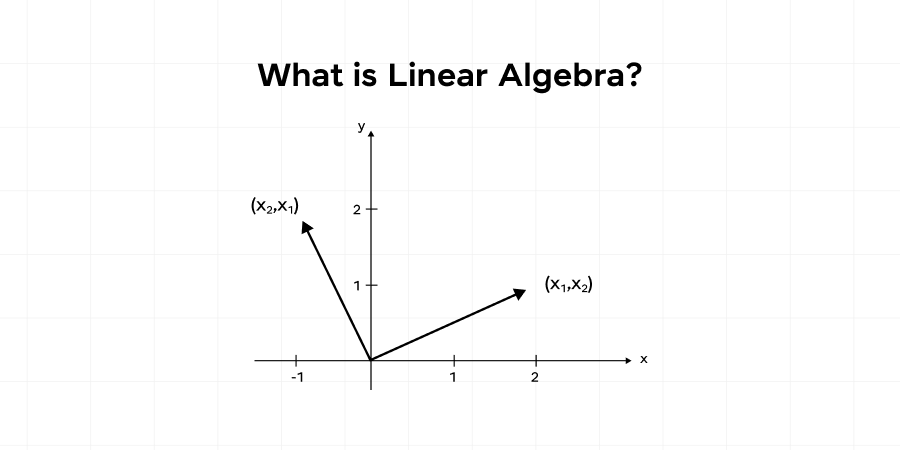
Key concepts in linear algebra include matrices, determinants, eigenvalues, and eigenvectors, which are essential for solving linear systems and transforming data.

Before we move into the next section, ensure you must have a good grip on data science essentials like Python, MongoDB, Pandas, NumPy, Tableau & PowerBI Data Methods. If you are looking for a detailed course on Data Science, you can join GUVI’s Data Science Course with Placement Assistance. You’ll also learn about the trending tools and technologies and work on some real-time projects.  

Additionally, if you want to explore Python through a self-paced course, try GUVI’s Python course.

Linear Algebra in Data Science

In relation to data science, linear algebra serves as a foundational tool for understanding and manipulating data. It allows data scientists to perform operations on datasets efficiently, understand the geometry of data, and implement various algorithms that are core to machine learning and data analysis.

Techniques like Principal Component Analysis (PCA) and Singular Value Decomposition (SVD) leverage linear algebra for dimensionality reduction, simplifying data while preserving key features. Overall, linear algebra’s principles are integral to understanding and implementing the algorithms that drive data science.

If you do not know how to begin your journey as a data scientist, you must follow a complete roadmap to become one.

Representation of Problems in Linear Algebra

Linear algebra is a powerful framework for representing and solving various mathematical and real-world problems. By translating these problems into systems of linear equations, matrices, and vectors, we can leverage the tools and techniques of linear algebra to find solutions efficiently. Here, we’ll explore some common ways problems are represented in linear algebra:

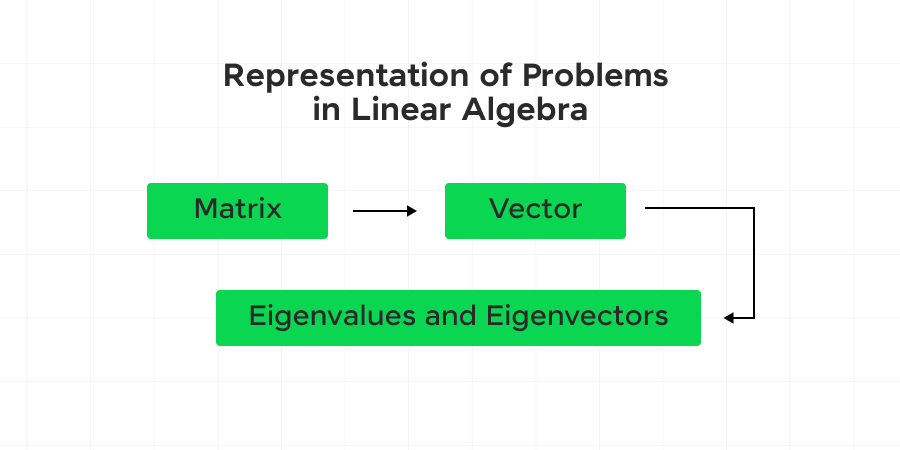
• Systems of Linear Equations: One of the most fundamental representations in linear algebra is the system of linear equations. A system of linear equations consists of multiple linear equations involving the same set of variables.
• Matrix Representation: Matrices are a central element in linear algebra and are used to represent data, transformations, and systems of equations. A matrix is a rectangular array of numbers arranged in rows and columns.
• Vector Representation: Vectors are essential components in linear algebra and represent points or directions in space. They can be column vectors (vertical) or row vectors (horizontal).
• Eigenvalues and Eigenvectors: Eigenvalues and eigenvectors are crucial in understanding linear transformations.

Importance of Linear Algebra in Data Science

Linear algebra is crucial in data science for several reasons, let’s understand a few:

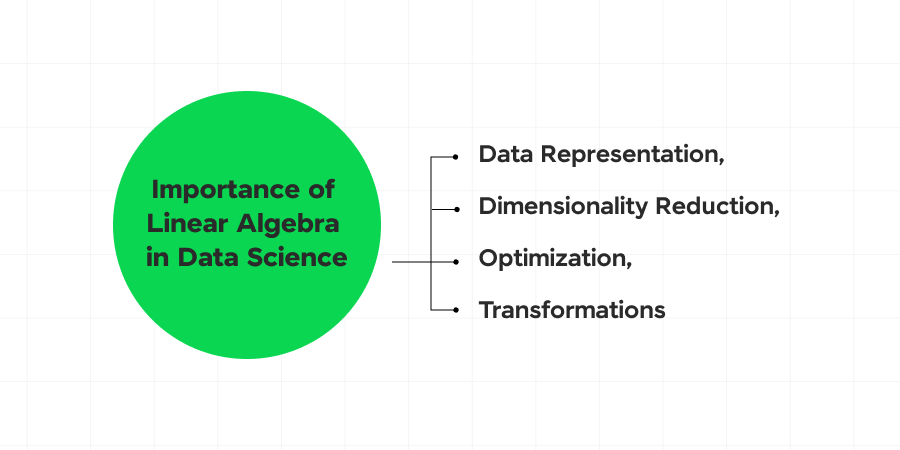
1. Data Representation: Datasets are often represented as matrices, where rows can represent samples and columns represent features. Understanding matrix operations is essential for manipulating and transforming data.
2. Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) rely on linear algebra to reduce the number of dimensions in a dataset while preserving as much variance as possible. This makes data analysis and visualization more manageable.
3. Optimization: Many machine learning algorithms, such as linear regression and support vector machines, involve optimization problems that are solved using linear algebra techniques.
4. Transformations: Operations such as rotations, translations, and scaling of data points in a feature space are mathematically described using linear algebra.

Applications of Linear Algebra in Data Science

Let’s look into some of the major applications of linear algebra in data science:

1. Principal Component Analysis (PCA): PCA is a technique used to reduce the dimensionality of data by transforming it into a new coordinate system. The new coordinates (principal components) are linear combinations of the original features, and they maximize the variance in the data.
2. Singular Value Decomposition (SVD): SVD is used in various applications, such as recommender systems and image compression. It decomposes a matrix into three other matrices, revealing the intrinsic structure of the data.
3. Linear Regression: One of the most common techniques in machine learning, linear regression, models the relationship between a dependent variable and one or more independent variables using a linear equation.
4. Neural Networks: The operations in neural networks, especially in the feedforward and backpropagation processes, involve matrix multiplications and other linear algebra operations.
5. Clustering Algorithms: Algorithms like K-means clustering use linear algebra to calculate distances between points and centroids, which is essential for grouping similar data points together.

Data Science also proves to be a promising career opportunity with growth and pays a great salary for every level,

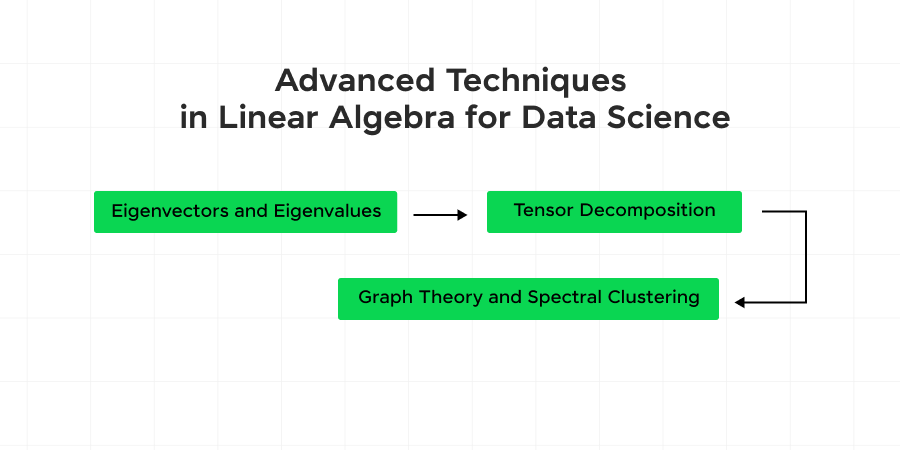
Advanced Techniques in Linear Algebra for Data Science

Also. read about some of the advanced techniques data scientists should know in linear algebra for data science:

1. Eigenvectors and Eigenvalues: These are used in many areas, including stability analysis and systems of differential equations. In data science, they are particularly important in PCA and for understanding linear transformation properties.
2. Matrix Factorization: Techniques such as Non-negative Matrix Factorization (NMF) are used in areas like topic modeling and collaborative filtering.
3. Tensor Decomposition: In more complex data structures, tensors (generalizations of matrices) are used. Tensor decomposition techniques help in uncovering latent patterns in multidimensional data.
4. Convex Optimization: Many machine learning algorithms involve solving optimization problems. Convex optimization problems, which have unique solutions, are particularly tractable and are often solved using linear algebra techniques.
5. Graph Theory and Spectral Clustering: Linear algebra plays a role in graph theory, particularly in the spectral clustering method, which involves the eigenvalues and eigenvectors of matrices derived from graphs.

Do work on some top projects on data science which would give a real-life understanding of the concepts.

Kickstart your Data Science journey by enrolling in GUVI’s Data Science Course where you will master technologies like MongoDB, Tableau, Power BI, Pandas, etc., and build interesting real-life projects.

Alternatively, if you would like to explore Python through a Self-paced course, try GUVI’s Python Certification course.

Wrap Up

Linear algebra is an indispensable tool in data science. Its concepts and techniques are foundational to many algorithms and methods used in data analysis, machine learning, and artificial intelligence.

A solid understanding of linear algebra not only enhances one’s ability to perform complex data manipulations but also provides deeper insights into the behavior and performance of various data science algorithms. As data continues to grow in size and complexity, the importance of linear algebra in data science will only continue to increase.

FAQs

How is linear algebra used in data science?

Linear Algebra in data science provides tools used for interacting with data in various ways, understanding relationships between variables, performing dimensionality reduction, and solving systems of equations.

Do you need to know linear algebra to be a data scientist?

Yes, Linear algebra is an important concept you should know in data science and machine learning. It provides the foundation for understanding and manipulating data efficiently.

Is linear algebra used in coding?

No, you do not need to know linear algebra in coding. Linear algebra is a mathematical concept that helps you to solve complex problems, not in the coding.