
Heap Data Structure Explained: Types, Operations, and Real-World Applications
Nov 26, 2025 11 Min Read 4114 Views
(Last Updated)
Ever wondered how computers decide which task to execute first when everything seems equally important? Well, the secret lies in a structure that organizes data not just by value but by priority: the Heap Data Structure. If you’ve ever dealt with sorting algorithms, optimized searches, or graph traversal techniques, you’ve likely encountered the efficiency that heaps bring to the table.
Curious to see how heaps work, the types that exist, and how to implement them in Python, C, Java, and C++? Continue reading this blog to explore their core operations, advantages, applications, and complete implementation examples step-by-step.
Table of contents
- What is Heap Data Structure?
- Main Types of Heap
- Other Types of Heap Data Structure
- Binomial Heap
- Fibonacci Heap
- Pairing Heap
- Min-Max Heap
- Core Operations of Heap Data Structure
- Heapify
- Insertion
- Deletion
- getMax (for Max-Heap) or getMin (for Min-Heap)
- Advantages of Heap Data Structure
- Efficient Access to Extremes
- Predictable Time Complexity
- Memory Efficiency
- Strong Foundation for Algorithms
- Adaptability Across Variations
- Applications of Heap Data Structure
- Priority Queues
- Heap Sort
- Graph Algorithms
- Event Simulation
- Order Statistics
- Step-by-Step Implementation of Heap Data Structure
- Step 1: Choose the Layout
- Step 2: Fix the Index Formulas
- Step 3: Build a Heap from Raw Data
- Step 4: Insert a New Key
- Step 5: Remove the Root
- Step 6: Adjust a Key Already in the Heap
- Step 7: Prove Correctness and Track Costs
- Heap Data Structure in Python
- Heap Data Structure in C
- Heap Data Structure in Java
- Heap Data Structure in C++
- Limitations of Heap Data Structure
- Conclusion
- FAQs
- What purpose does a heap serve in data structures?
- How does a heap differ from a binary search tree?
- Where is a heap used in practical systems?
- Which operations define the behavior of a heap?
- Can heaps be built in different programming languages?
What is Heap Data Structure?
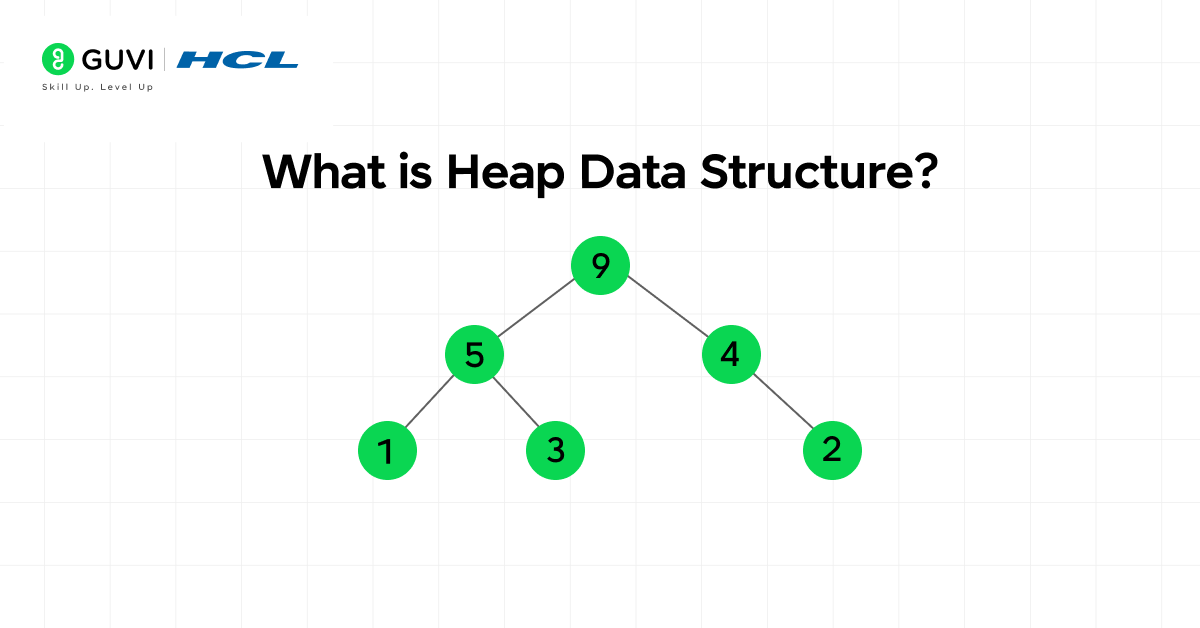
A heap is a specialized tree-based data structure that maintains a specific order property between parent and child nodes. It operates as a complete binary tree, which means all levels are filled except possibly the last, and the last level’s nodes are aligned toward the left.
In a max heap, each parent node has a value greater than or equal to its children, whereas in a min heap, the parent’s value is smaller or equal. This structure allows efficient access to the highest or lowest value in constant time. The same structure makes heaps particularly effective for priority queues and memory management.
Main Types of Heap
The two main types are Min-Heap and Max-Heap, which differ in how they organize and retrieve data within the tree.
| Heap Type | Definition | Root Property | Use Case | Time Complexity (Insertion / Deletion / Access) |
| Min-Heap | Each parent node has a value smaller than or equal to its children. | Root always holds the smallest element. | Used in algorithms like Dijkstra’s shortest path, Prim’s MST, and event scheduling. | O(log n) / O(log n) / O(1) |
| Max-Heap | Each parent node has a value greater than or equal to its children. | Root always holds the largest element. | Used in heap sort, process scheduling, and systems requiring frequent access to maximum values. | O(log n) / O(log n) / O(1) |
Other Types of Heap Data Structure
1. Binomial Heap
A binomial heap is composed of multiple binomial trees linked together according to their order. It efficiently supports merging operations between heaps.
Key Features:
- Supports heap merging in O(log n) time.
- Each binomial tree follows a strict structural order.
- Useful in systems that require frequent union operations, such as memory and task management.
- Provides efficient performance for insert and delete-min operations.
Read: Ultimate Guide 2025: Difference Between Data Structures and Algorithms Explained
2. Fibonacci Heap
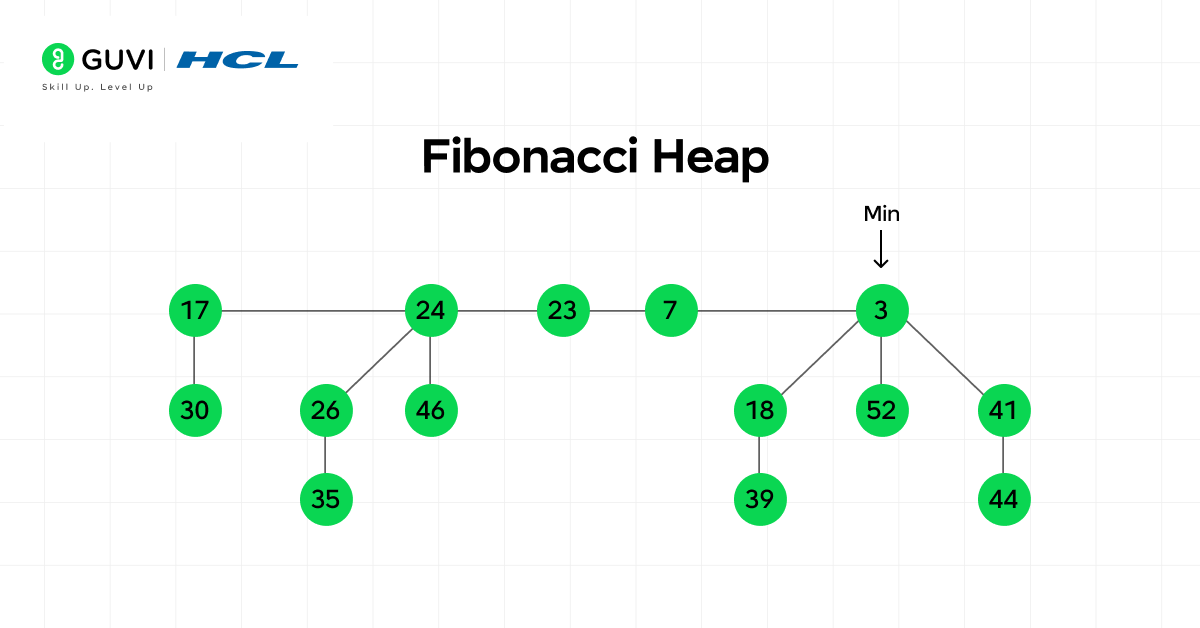
A Fibonacci heap uses a collection of trees with a relaxed structure to achieve excellent amortized performance. It is well-suited for data exploration and algorithms that perform many key updates.
Key Features:
- Offers O(1) amortized time for insertion and decrease-key operations.
- Performs merge operations efficiently.
- Commonly used in graph algorithms that involve frequent key adjustments.
- Maintains a flexible and loosely connected structure that reduces rebalancing costs.
3. Pairing Heap
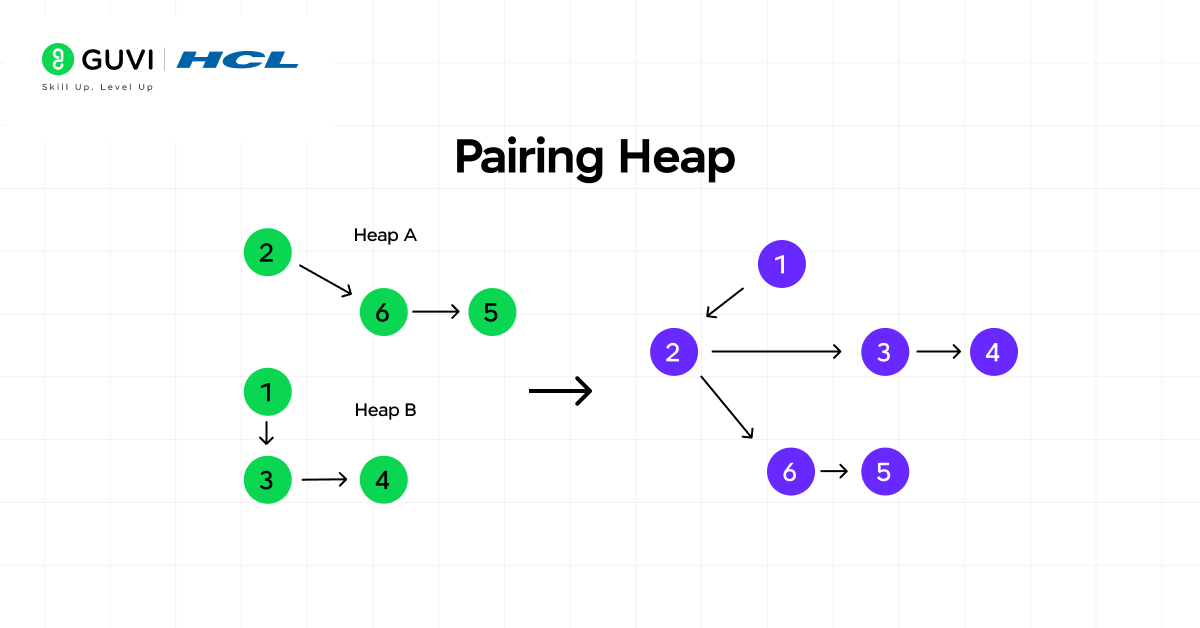
A pairing heap is a simple and practical heap implementation that uses a multiway tree and repeated pairing to maintain order.
Key Features:
- Simple to implement with strong empirical performance.
- Performs merge and decrease-key operations efficiently in practice.
- Works well in priority queue scenarios where key updates occur frequently.
- Balances simplicity with effective runtime behavior in real applications.
4. Min-Max Heap
A min-max heap combines the characteristics of both min-heaps and max-heaps. It alternates between minimum and maximum properties at different tree levels.
Key Features:
- Provides direct access to both smallest and largest elements in O(1) time.
- Even levels follow the min-heap property, and odd levels follow the max-heap property.
- Suitable for double-ended priority queues and range-based queries.
- Maintains balanced complexity with O(log n) for insertion and deletion.
Also, read: DSA for System Design: A Beginner’s Guide 2025
Core Operations of Heap Data Structure
1. Heapify
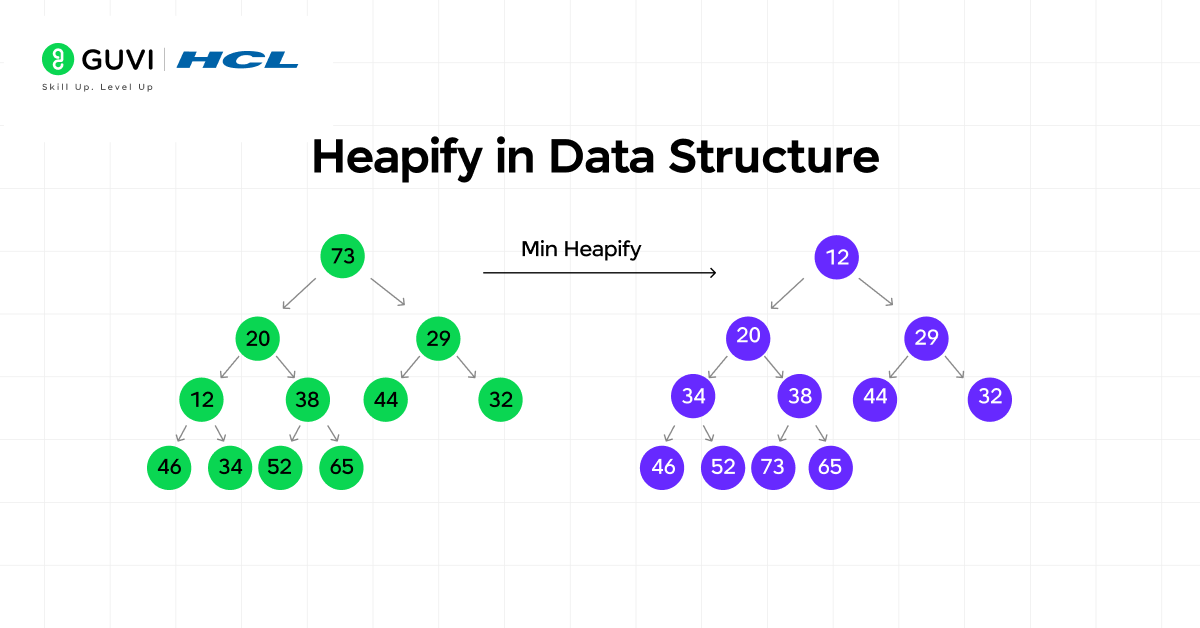
Heapify serves as the mechanism that restores order whenever the heap property is disturbed. It functions as the self-correcting feature of the structure. The operation activates after removing the root or during heap construction. When the root is replaced by the last element, heapify travels downward, comparing parents and children until the rule is satisfied again.
During heap building, heapify starts from the last internal node and moves upward to make sure all subtrees follow the property. The process runs in O(log n) time, which balances speed with structural accuracy. In a max-heap, it positions the largest element at the root, whereas in a min-heap, it ensures the smallest value remains there.
2. Insertion
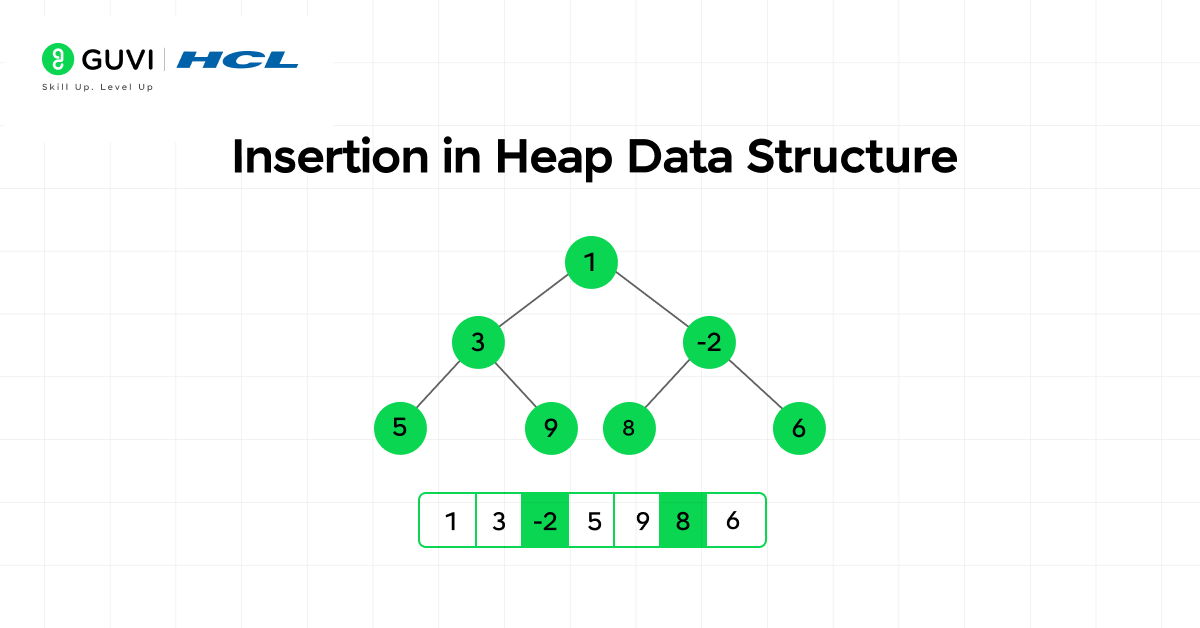
Insertion expands the heap while preserving its completeness. The new element is first added at the lowest available position. If the insertion disrupts the order, a heapify-up operation compares the new element with its parent and swaps them as needed until order is restored. This controlled movement keeps the tree’s shape consistent and guarantees that the property holds across all levels. The entire process completes in O(log n) time, providing a steady and efficient insertion rate even as data grows.
3. Deletion
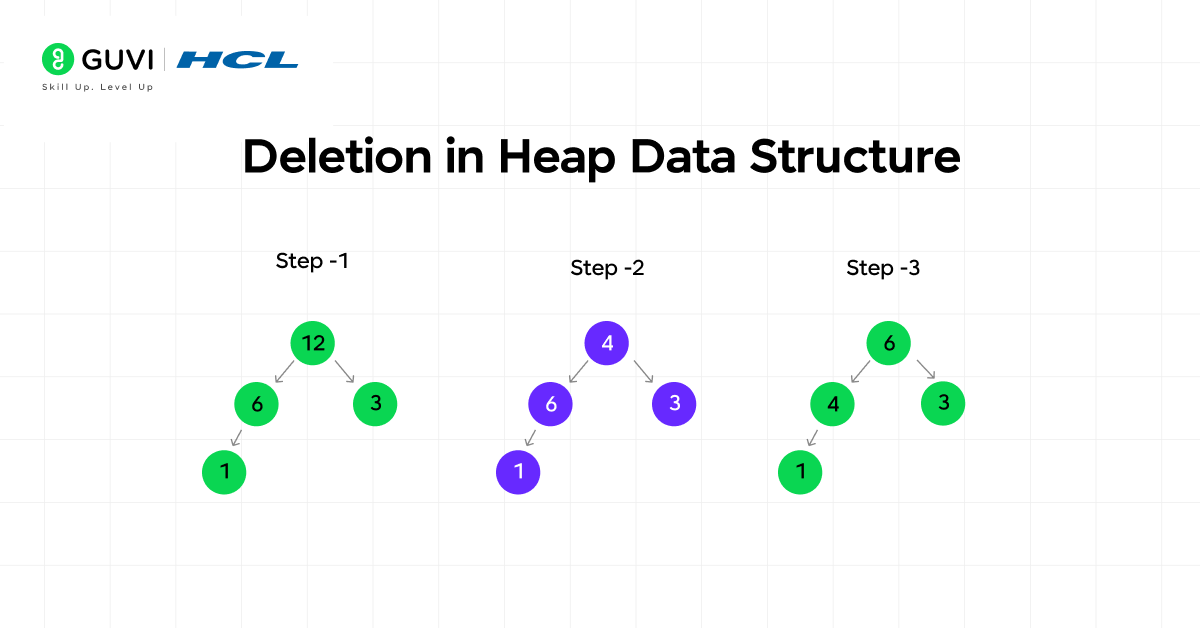
Deletion focuses on removing the root while keeping the structure balanced. The last element replaces the root to maintain completeness, followed by a heapify-down operation that restores order from the top down. Each swap rebuilds the hierarchy so that the heap’s defining rule remains intact. This operation also runs in O(log n) time, which maintains efficiency even in large heaps where repeated removals are required.
4. getMax (for Max-Heap) or getMin (for Min-Heap)
Retrieving the root is the simplest operation because the extreme value always sits at the top. A max-heap returns the largest value, and a min-heap returns the smallest. Since no rearrangement or traversal is needed, access occurs instantly in O(1) time. This direct access is what makes heaps a natural choice for systems that require constant monitoring of priority elements such as job queues or event simulations.
Advantages of Heap Data Structure
1. Efficient Access to Extremes
A heap gives direct access to either the smallest or largest element depending on its type. This ability keeps retrieval immediate, which supports time-critical operations such as process scheduling and real-time task management. Systems that rely on constant priority updates benefit from this predictable access pattern.
2. Predictable Time Complexity
Insertion and deletion always follow a logarithmic growth pattern relative to the number of elements. This stable behavior allows programmers to plan algorithm performance with accuracy. Large data operations stay consistent in speed, which reduces processing delays in practical applications.
3. Memory Efficiency
Heaps use a compact array layout that avoids pointer-based navigation. The continuous arrangement in memory improves cache locality and minimizes fragmentation. This efficiency helps software systems handle intensive data operations with limited memory use.
4. Strong Foundation for Algorithms
Heaps form the backbone of sorting and pathfinding techniques. Their predictable order property allows algorithms to process data in controlled sequences. Structures like priority queues and search trees often depend on heaps to maintain balance and quick retrieval.
5. Adaptability Across Variations
Binary, binomial, and Fibonacci heaps each respond to different operational demands. Some favor faster merges while others focus on reducing update costs. This flexibility gives developers the option to align the heap design with the workload it supports.
Applications of Heap Data Structure
1. Priority Queues
A heap in data structure is widely used to implement priority queues where each element is assigned a priority value. The element with the highest or lowest priority is always accessed first. This structure supports quick retrieval and adjustment of priorities, which helps in handling processes such as job scheduling, event simulation, and bandwidth management.
2. Heap Sort
Heap sort uses the heap property to arrange elements in ascending or descending order. The algorithm first converts the dataset into a heap, extracts the root repeatedly, and rebuilds the heap after each extraction. This process creates a well-ordered sequence with a predictable time complexity. The same process makes it a dependable sorting technique for systems that require consistent performance.
3. Graph Algorithms
Heaps are essential in graph-based algorithms such as Dijkstra’s shortest path and Prim’s minimum spanning tree. They help in selecting the next edge or vertex with the minimum cost efficiently. Their logarithmic insertion and extraction times allow these algorithms to handle large graphs with accuracy and speed.
4. Event Simulation
Simulation software often schedules future events according to their timestamps or urgency levels. A min-heap stores these events so that the nearest future event always remains at the top. This organization keeps the simulation timeline accurate and computationally efficient.
5. Order Statistics
Heaps in DSA help in identifying the kth largest or smallest element in a dataset without performing a full sort. This approach is valuable in analytical applications where only a subset of ordered data is required. Their structured behavior within data structures and algorithms (DSA) ensures time efficiency and predictable performance across varied computational tasks.
Want to build AI-powered applications that perform under pressure? Enroll in our AI Software Development Course and learn how to integrate models, design APIs, deploy scalable systems, and optimize performance, even when things get heavy. Dive into hands-on projects, industry best practices, and production-ready workflows to turn your AI ideas into real solutions.
Step-by-Step Implementation of Heap Data Structure
Step 1: Choose the Layout
A heap uses a zero-indexed array to store its elements. This layout makes traversal and updates easier because the parent–child relationships follow direct index formulas.
Example:
If you insert values [10,5,3], they are stored as an array in the same order. This represents a complete binary tree where 10 is the root, 5 is the left child, and 3 is the right child.
Step 2: Fix the Index Formulas
For any element at index i, its parent is at ⌊(i−1)/2⌋, its left child at 2i+1, and its right child at 2i+2. These relationships keep the tree consistent.
Example:
If the heap array is [10,7,5,3,2], the element 7 is at index 1. Its parent is 10 at index 0, and its children are 3 and 2 at indices 3 and 4.
Step 3: Build a Heap from Raw Data
Turn an unsorted array into a heap using heapify-down from the last internal node up to the root.
Example:
Given [3,10,5,6,2], start heapifying from index 1 (value 10). After applying heapify-down, the max-heap becomes [10,6,5,3,2]. This process completes in O(n) time.
Step 4: Insert a New Key
Add the new value at the end to maintain completeness. Then use heapify-up to restore the heap property by comparing with its parent and swapping if required.
Example:
Inserting 8 into [10,6,5,3,2] gives [10,6,5,3, 2,8]. Since 8 is smaller than its parent 5 in a max-heap, a swap occurs, and the array becomes [10,8,6,3,2,5].
Step 5: Remove the Root
The root is removed, and the last element replaces it. Then heapify-down restores order.
Example:
Removing the root 10 from [10,8,6,3,2,5] places 5 at the top, giving [5,8,6,3,2]. After heapify-down, the heap becomes [8,5,6,3,2].
Step 6: Adjust a Key Already in the Heap
If a value changes, use heapify-up or heapify-down depending on whether it increased or decreased.
Example:
If the heap is [10,8,6,3,2] and the value 8 becomes 12, it swaps upward until the heap property holds, resulting in [12,10,6,3,2].
Step 7: Prove Correctness and Track Costs
Each operation maintains the heap’s structure and order. Heapify-up and heapify-down fix violations along one branch only, keeping the cost predictable.
Example:
Accessing the root takes O(1), inserting or deleting an element takes O(log n), and building a heap from raw data takes O(n). These properties make heaps reliable for tasks that depend on efficient priority handling.
Heap Data Structure in Python
class MaxHeap:
def __init__(self):
self.heap = []
def insert(self, val):
self.heap.append(val)
self._heapify_up(len(self.heap) – 1)
def delete(self):
if len(self.heap) > 1:
self._swap(0, len(self.heap) – 1)
max_val = self.heap.pop()
self._heapify_down(0)
elif self.heap:
max_val = self.heap.pop()
else:
max_val = None
return max_val
def _heapify_up(self, index):
parent = (index – 1) // 2
if index > 0 and self.heap[index] > self.heap[parent]:
self._swap(index, parent)
self._heapify_up(parent)
def _heapify_down(self, index):
largest = index
left = 2 * index + 1
right = 2 * index + 2
if left < len(self.heap) and self.heap[left] > self.heap[largest]:
largest = left
if right < len(self.heap) and self.heap[right] > self.heap[largest]:
largest = right
if largest != index:
self._swap(index, largest)
self._heapify_down(largest)
def _swap(self, i, j):
self.heap[i], self.heap[j] = self.heap[j], self.heap[i]
# Example usage
heap = MaxHeap()
heap.insert(10)
heap.insert(20)
heap.insert(5)
print(heap.heap) # Output: [20, 10, 5]
print(heap.delete()) # Output: 20
print(heap.heap) # Output: [10, 5]
Heap Data Structure in C
#include <stdio.h>
#include <stdlib.h>
#define MAX_HEAP_SIZE 100
typedef struct {
int size;
int data[MAX_HEAP_SIZE];
} MaxHeap;
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
void heapify_up(MaxHeap *heap, int index) {
int parent = (index – 1) / 2;
if (index > 0 && heap->data[index] > heap->data[parent]) {
swap(&heap->data[index], &heap->data[parent]);
heapify_up(heap, parent);
}
}
void heapify_down(MaxHeap *heap, int index) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heap->size && heap->data[left] > heap->data[largest]) {
largest = left;
}
if (right < heap->size && heap->data[right] > heap->data[largest]) {
largest = right;
}
if (largest != index) {
swap(&heap->data[index], &heap->data[largest]);
heapify_down(heap, largest);
}
}
void insert(MaxHeap *heap, int val) {
if (heap->size == MAX_HEAP_SIZE) {
printf(“Heap is full\n”);
return;
}
heap->data[heap->size] = val;
heap->size++;
heapify_up(heap, heap->size – 1);
}
int delete(MaxHeap *heap) {
if (heap->size == 0) {
printf(“Heap is empty\n”);
return -1;
}
int max_val = heap->data[0];
heap->data[0] = heap->data[heap->size – 1];
heap->size–;
heapify_down(heap, 0);
return max_val;
}
int main() {
MaxHeap heap;
heap.size = 0;
insert(&heap, 10);
insert(&heap, 20);
insert(&heap, 5);
for (int i = 0; i < heap.size; i++) {
printf(“%d “, heap.data[i]);
}
printf(“\n”);
printf(“Deleted: %d\n”, delete(&heap));
for (int i = 0; i < heap.size; i++) {
printf(“%d “, heap.data[i]);
}
printf(“\n”);
return 0;
}
Heap Data Structure in Java
import java.util.ArrayList;
import java.util.List;
class MaxHeap {
private List<Integer> heap;
public MaxHeap() {
heap = new ArrayList<>();
}
public void insert(int val) {
heap.add(val);
heapifyUp(heap.size() – 1);
}
public int delete() {
if (heap.isEmpty()) {
throw new IllegalStateException(“Heap is empty”);
}
int root = heap.get(0);
heap.set(0, heap.get(heap.size() – 1));
heap.remove(heap.size() – 1);
heapifyDown(0);
return root;
}
private void heapifyUp(int index) {
int parent = (index – 1) / 2;
if (index > 0 && heap.get(index) > heap.get(parent)) {
swap(index, parent);
heapifyUp(parent);
}
}
private void heapifyDown(int index) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heap.size() && heap.get(left) > heap.get(largest)) {
largest = left;
}
if (right < heap.size() && heap.get(right) > heap.get(largest)) {
largest = right;
}
if (largest != index) {
swap(index, largest);
heapifyDown(largest);
}
}
private void swap(int i, int j) {
int temp = heap.get(i);
heap.set(i, heap.get(j));
heap.set(j, temp);
}
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
heap.insert(10);
heap.insert(20);
heap.insert(5);
System.out.println(heap.heap); // Output: [20, 10, 5]
System.out.println(heap.delete()); // Output: 20
System.out.println(heap.heap); // Output: [10, 5]
}
}
Heap Data Structure in C++
#include <iostream>
#include <vector>
#include <stdexcept>
using namespace std;
class MaxHeap {
public:
void insert(int val) {
heap.push_back(val);
heapifyUp(heap.size() – 1);
}
int deleteMax() {
if (heap.empty()) {
throw out_of_range(“Heap is empty”);
}
int maxVal = heap.front();
heap.front() = heap.back();
heap.pop_back();
heapifyDown(0);
return maxVal;
}
void printHeap() {
for (int val : heap)
cout << val << ” “;
cout << endl;
}
private:
vector<int> heap;
void heapifyUp(int index) {
int parent = (index – 1) / 2;
if (index > 0 && heap[index] > heap[parent]) {
swap(heap[index], heap[parent]);
heapifyUp(parent);
}
}
void heapifyDown(int index) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heap.size() && heap[left] > heap[largest])
largest = left;
if (right < heap.size() && heap[right] > heap[largest])
largest = right;
if (largest != index) {
swap(heap[index], heap[largest]);
heapifyDown(largest);
}
}
};
int main() {
MaxHeap heap;
heap.insert(10);
heap.insert(20);
heap.insert(5);
heap.printHeap(); // Output: 20 10 5
cout << heap.deleteMax() << endl; // Output: 20
heap.printHeap(); // Output: 10 5
return 0;
}
Want to go beyond understanding heaps and actually build them from scratch? Learn how heaps power sorting algorithms, graph optimizations, and system schedulers with our Data Structures & Algorithms using Java Course. Strengthen your algorithmic foundations, code Min-Heaps and Max-Heaps hands-on, and master problem-solving patterns used in top product companies. Build the confidence to tackle coding interviews and real-world performance challenges with structured DSA training.
Limitations of Heap Data Structure
- Costly Search Operations: A heap allows quick access to the extreme element but offers no direct path to locate arbitrary values. Searching for a specific element requires traversing the entire structure, which results in linear time complexity. This limits its usefulness in applications that rely on frequent random searches.
- Unstable Order Among Siblings: Elements at the same level do not follow any defined order, which means the heap provides partial rather than total sorting. Extracting elements one by one will produce a sorted sequence, yet the structure itself does not maintain that state internally. This behavior can cause additional processing if ordered traversal is needed.
- Complex Implementation for Advanced Variants: Structures like Fibonacci or binomial heaps offer improved theoretical performance but require detailed pointer management and careful coding. Small implementation errors can break the heap property and cause inconsistent results. Developers often prefer simpler binary heaps despite the potential efficiency trade-off.
- High Constant Factors in Some Operations: Although most operations stay logarithmic in complexity, the hidden constant factors can be large, especially in variants that use multiple trees or auxiliary structures. In practical environments where latency matters, these constants may offset theoretical gains.
- Limited Support for Sequential Data Access: In a DSA roadmap, heaps are designed for quick access to priority elements rather than for ordered data traversal. Sequential access to elements requires repeated extraction, which breaks the heap structure during the process. This behavior makes heaps less suitable for cases that demand both fast access and consistent ordering of data.
Conclusion
The heap data structure stands as a practical solution for problems that demand efficient ordering and retrieval of elements. Its proficiency to strengthen structured relationships between parent and child nodes is unmatched. It allows it to perform tasks such as sorting, prioritizing, and managing memory with consistency and speed. Heaps form a crucial link between theory and application, as it supports systems that must make quick decisions with limited computational effort.
FAQs
1. What purpose does a heap serve in data structures?
A heap manages data where each element carries a priority. It lets systems access either the smallest or largest element instantly, which keeps operations such as scheduling and sorting efficient under growing workloads.
2. How does a heap differ from a binary search tree?
A heap focuses on maintaining a consistent relationship between parents and children. A binary search tree maintains an ordered structure across every level, while a heap preserves order only along each branch, which makes retrieval of priority elements faster.
3. Where is a heap used in practical systems?
Heaps appear in systems that handle real-time scheduling, shortest path selection, and task prioritization. They also support data compression and memory allocation processes where quick access to a minimum or maximum value matters.
4. Which operations define the behavior of a heap?
A heap depends on operations that keep its structure valid. Insertion, deletion, and heapify work together to maintain the hierarchy. Each action adjusts the tree carefully so that its defining order remains stable with logarithmic performance.
5. Can heaps be built in different programming languages?
Heaps can be written in Python, C, Java, or C++. Each language offers its own syntax and structure, but the logic behind heap creation stays the same. Understanding this shared foundation helps developers handle data efficiently across environments.

























Did you enjoy this article?