
DSA with Python: Understand the Foundations of Coding
Oct 10, 2025 6 Min Read 2905 Views
(Last Updated)
Have you ever wondered what separates a good programmer from a great one? It often boils down to how well they understand Data Structures and Algorithms (DSA).
And if you’re choosing Python as your weapon of choice, you’re already on a powerful path. But how do you combine DSA with Python effectively?
In this article, we’ll explore how Python can be used to master DSA, especially for competitive programming, and why it matters so much in both learning and real-world problem-solving. So, without further ado, let us get started!
Table of contents
- What is DSA and Why Should You Care?
- Why DSA With Python?
- Core Data Structures in Python
- Lists (Dynamic Arrays)
- Tuples (Immutable Lists)
- Sets (Unordered Unique Elements)
- Dictionaries (Hash Maps)
- Stacks
- Queues
- Linked Lists (Manual Implementation)
- Core Algorithms in Python
- Searching Algorithms
- Sorting Algorithms
- Recursion & Backtracking
- Dynamic Programming (DP)
- Roadmap to Learn DSA with Python (12-Week Plan)
- Phase 1: Beginner (Weeks 1–3)
- Phase 2: Intermediate (Weeks 4–8)
- Phase 3: Advanced (Weeks 9–12)
- Conclusion
- FAQs
- What exactly is DSA with Python?
- Why is Python a good choice for learning DSA?
- What core data structures and algorithms should I master first?
- How do I measure efficiency in Python DSA?
- Where should I practice Python‑based DSA problems?
What is DSA and Why Should You Care?

Data Structures and Algorithms (DSA) form the foundation of computer science. Here’s a simple way to think about them:
- Data Structures help you organize data efficiently.
- Algorithms help you process that data quickly and correctly.
Together, they enable your code to be both elegant and efficient.
Whether you’re aiming to ace coding interviews, participate in hackathons, or solve real-world problems, understanding DSA is non-negotiable.
Why DSA With Python?
You might hear people say, “Python is slow.” While that’s partially true compared to languages like C++, Python shines in readability, simplicity, and community support. That makes it a fantastic choice for learning DSA.
Key Advantages:
- Built-in data types like list, set, dict, and tuple
- Rich libraries like collections, heapq, bisect, and itertools
- Readable syntax, making complex algorithms easier to write and debug
Let’s dive deeper into Python-powered DSA.
Core Data Structures in Python
Understanding data structures is crucial for writing optimized and scalable code. In Python, you have access to several built-in and abstract data structures that make solving problems easier and more intuitive.
Let’s explore each of the core data structures in depth.
1. Lists (Dynamic Arrays)
Python’s list is an ordered, dynamic array. It can hold items of any data type and allows random access via indexing.
Key Operations:
arr = [1, 2, 3]
arr.append(4) # Add to end
arr.insert(1, 10) # Insert at index
arr.pop() # Remove from end
arr.remove(10) # Remove specific element
print(arr[2]) # Access by index
Use Cases:
- Storing elements in a sequence
- Two-pointer problems
- Prefix/suffix sums
- Sliding window
2. Tuples (Immutable Lists)
Tuple is a fixed-size, immutable sequence. Once created, its values cannot be changed.
coordinates = (10, 20)
print(coordinates[0]) # Output: 10
Why Use It?
- Safer than lists when mutability is not needed
- Hashable → Can be used as keys in dict and elements in set
Use Cases:
- Storing a fixed group of related items
- Returning multiple values from a function
3. Sets (Unordered Unique Elements)
A set is an unordered collection of unique elements. It’s implemented using a hash table.
my_set = {1, 2, 3}
my_set.add(4)
my_set.remove(2)
print(3 in my_set) # Output: TrueUse Cases:
- Checking membership
- Removing duplicates
- Set operations (union, intersection, difference)
4. Dictionaries (Hash Maps)
A dict is a collection of key-value pairs. Like a set, it is backed by a hash table.
student = {'name': 'Alice', 'age': 20}
student['grade'] = 'A'
print(student.get('age')) # Output: 20Use Cases:
- Storing mapping data (e.g., word → frequency)
- Caching/memoization
- Fast lookups
5. Stacks
A stack is a LIFO (Last-In, First-Out) structure. Python doesn’t have a built-in stack type, but you can use a list or deque.
stack = []
stack.append(1)
stack.append(2)
print(stack.pop()) # Output: 2Use Cases:
- Undo functionality
- Parsing expressions
- Depth-first search
6. Queues
A queue is FIFO (First-In, First-Out). For optimal performance, use collections.deque instead of list.
from collections import deque
queue = deque()
queue.append(1)
queue.append(2)
print(queue.popleft()) # Output: 1Use Cases:
- BFS traversal in graphs
- Scheduling and task execution
- Buffering
7. Linked Lists (Manual Implementation)
Python doesn’t have built-in linked lists, so we usually implement them ourselves.
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def insert(self, data):
new = Node(data)
new.next = self.head
self.head = newUse Cases:
- Efficient insert/delete at head
- Implementing stacks/queues
- Collision handling in hash tables (chaining)
While lists in Python offer dynamic arrays, linked lists give better control in low-level operations, but they’re mostly used in interviews and system-level programming.
Core Algorithms in Python
Once you understand data structures, the next logical step is learning algorithms, the step-by-step logic to solve problems. Python’s clean syntax makes it perfect for implementing and understanding them.
Below are the key algorithm types you should know:
1. Searching Algorithms
Searching algorithms are the foundation of many real-world applications, from database lookups to file searches. In Python, searching can be done in simple or optimized ways.
Linear Search
Linear Search is the most straightforward approach, scanning each element until the target is found. Searches each element one by one. Simple but inefficient for large datasets.
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1Time Complexity: O(n)
Binary Search
Binary Search, on the other hand, leverages the power of divide and conquer to drastically reduce search time in sorted arrays, making it ideal for performance-critical scenarios. Only works on sorted arrays. Divide and conquer logic.
def binary_search(arr, target):
low, high = 0, len(arr) - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1Time Complexity: O(log n)
2. Sorting Algorithms
Sorting is a critical step in data processing and often a prerequisite for other algorithms like binary search or optimization tasks. Python allows you to implement classic sorting techniques such as Bubble Sort, Merge Sort, and Quick Sort with elegant syntax.
Bubble Sort
Bubble Sort is one of the simplest sorting algorithms that works by repeatedly swapping adjacent elements if they are in the wrong order. It “bubbles” the largest elements to the end with each pass.
While it’s not efficient for large datasets, it’s great for beginners to understand the concept of sorting logic.
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]Time Complexity: O(n²)
Merge Sort
Merge Sort is a classic example of the divide-and-conquer approach. It splits the array into halves, recursively sorts them, and then merges the sorted halves. It’s efficient and stable, with a consistent time complexity of O(n log n), making it suitable for large datasets.
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr)//2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
merged, i, j = [], 0, 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
merged.append(left[i])
i += 1
else:
merged.append(right[j])
j += 1
return merged + left[i:] + right[j:]Time Complexity: O(n log n)
Quick Sort
Quick Sort is another divide-and-conquer algorithm that picks a pivot, partitions the array around it, and then recursively sorts the partitions. It’s known for being fast in practice, though its worst-case time complexity is O(n²).
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[0]
lesser = [x for x in arr[1:] if x < pivot]
greater = [x for x in arr[1:] if x >= pivot]
return quick_sort(lesser) + [pivot] + quick_sort(greater)Time Complexity: Average: O(n log n) | Worst: O(n²)
3. Recursion & Backtracking
Recursion is a technique where a function calls itself to solve subproblems. It’s commonly used in tree traversal, mathematical computations, and exploring all possible outcomes.
Example: Factorial
def factorial(n):
return 1 if n == 0 else n * factorial(n - 1).4. Dynamic Programming (DP)
Dynamic Programming is a powerful algorithmic paradigm used to solve problems with overlapping subproblems and optimal substructure. It’s especially useful in scenarios where brute force would be too slow, like calculating Fibonacci numbers, solving the 0/1 knapsack problem, or finding the longest common subsequence.
Fibonacci with Memoization
def fib(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fib(n-1, memo) + fib(n-2, memo)
return memo[n]Common in optimization problems, like:
- Longest Common Subsequence
- Knapsack
- Matrix Chain Multiplication
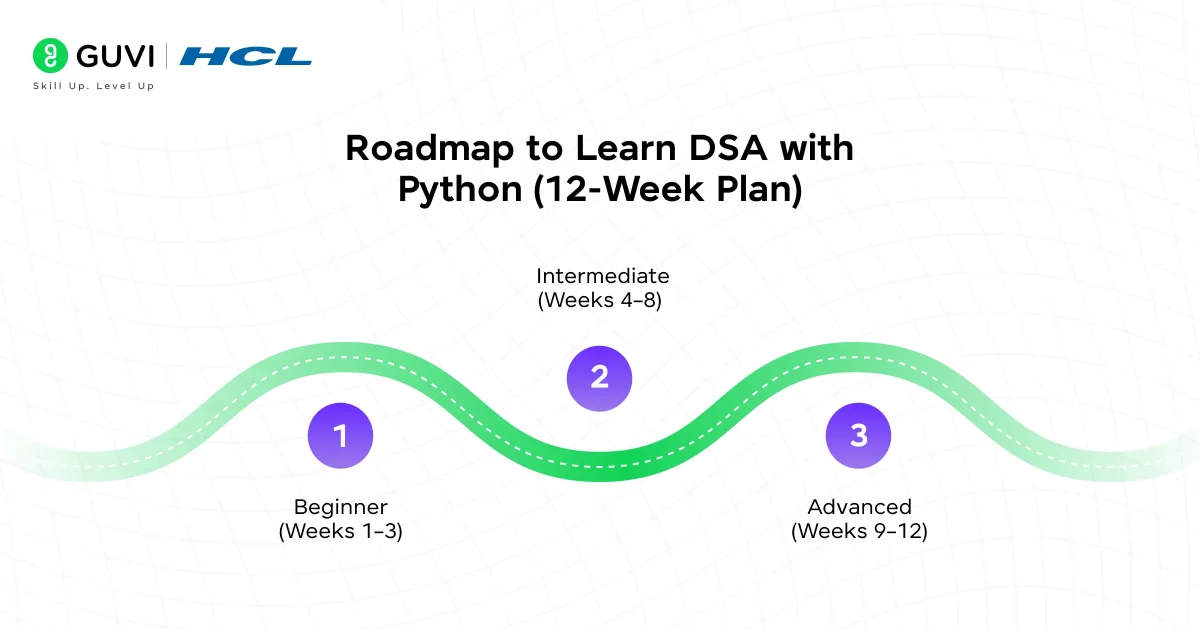
Roadmap to Learn DSA with Python (12-Week Plan)
- Total Duration: 12 Weeks
- Goal: Build strong foundations, improve problem-solving, and become interview-ready using Python
- Time Commitment: 1.5 to 2 hours/day (flexible)
Phase 1: Beginner (Weeks 1–3)
Objective: Grasp basic data structures, problem-solving logic, and Python syntax
| Week | Topics Covered | Practice Goals |
| Week 1 | Arrays and StringsList operationsBasic Looping & Conditions | Solve 20+ problems on arrays & strings |
| Week 2 | Stack & QueueSliding Window PatternHashing Basics (dict, set) | 15 stack/queue questionsLearn deque, Counter, and defaultdict |
| Week 3 | Recursion BasicsPrefix SumTwo-Pointer Technique | Practice recursive functions10+ problems on two pointers/sliding window |
Phase 2: Intermediate (Weeks 4–8)
Objective: Tackle more complex data structures and standard algorithms
| Week | Topics Covered | Practice Goals |
| Week 4 | Linked Lists (Singly & Doubly)Implement from scratch | Solve 10–15 LL problems on reversal, middle node, merge |
| Week 5 | Trees: Inorder, Preorder, PostorderDFS, BFS basics | 15+ tree problemsVisualize traversal |
| Week 6 | Binary Search (on arrays & answers)Sorting Algorithms | Implement Merge, Quick, and Heap sort20 binary search questions |
| Week 7 | HashMaps in depthProblems like Anagrams, Two Sum | Practice map-based problems |
| Week 8 | Greedy AlgorithmsInterval Problems | 10 classic greedy problems (activity selection, coin change, etc.) |
Phase 3: Advanced (Weeks 9–12)
Objective: Master optimization techniques and handle complex real-world problems
| Week | Topics Covered | Practice Goals |
| Week 9 | Dynamic Programming (DP Basics)Memoization vs Tabulation | Solve Fibonacci, LCS, Knapsack10 DP problems |
| Week 10 | BacktrackingCombinations & Permutations | N-Queens, Sudoku solver, Subsets |
| Week 11 | Graphs: DFS, BFSAdjacency list/matrix | BFS/DFS on matrix & connected components |
| Week 12 | Dijkstra’s AlgorithmTopological SortTries (Basics) | Implement using heapq and defaultdict5 problems each |
By following this roadmap, you can easily learn DSA with Python, and the best part about this is that you don’t need to get confused on where to start, just follow this plan and attain your end goal of strengthening your coding foundation!
So, after reading all this, if you are ready to start your journey in learning Data Structures and Algorithms, consider enrolling in HCL GUVI’s Data Structures and Algorithms Course with Python – IIT-M Pravartak Certified, which includes four in-depth courses across Python, Java, C, and JavaScript. It also helps you to master algorithmic problem-solving and prepare for technical interviews with industry-grade certification!
Conclusion
In conclusion, mastering DSA with Python is more than just a checkbox for interviews; it’s a mindset shift in how you approach problems. Python’s simplicity, combined with its powerful libraries and readability, makes it a perfect language to learn and implement core algorithmic concepts efficiently.
So start small, be consistent, and build one problem at a time; your future as a strong, Python-powered problem solver is just a few lines of clean logic away.
FAQs
1. What exactly is DSA with Python?
It’s the practice of using Data Structures (like lists, trees, graphs) and Algorithms (search, sort, DP, etc.) implemented in Python to solve programming problems efficiently. Python’s built‑in types and libraries make it easy to learn and apply computational logic for tasks like competitive programming, interview prep, and real‑world applications.
2. Why is Python a good choice for learning DSA?
Python boasts readable syntax and powerful modules—like collections, heapq, and bisect—so you can focus more on algorithmic logic and less on boilerplate coding. Its dynamic typing and built‑in data types make it perfect for prototyping and iterating over your DSA solutions quickly.
3. What core data structures and algorithms should I master first?
Start with essentials like arrays (lists), stacks, queues, hash tables (dict/set), and basic algorithms like linear/binary search, sorting, recursion, and graph traversal (DFS/BFS). These build the foundation for solving most intermediate to advanced problems effectively.
4. How do I measure efficiency in Python DSA?
You analyze your code using Big-O notation to estimate time and space complexity. For example, list indexing is O(1), but searching is O(n), whereas dictionary lookups are also O(1). Understanding these trade-offs helps you write scalable solutions.
5. Where should I practice Python‑based DSA problems?
Platforms like LeetCode, HackerRank, GeeksforGeeks, and CodeChef offer problem sets that let you filter by both topic and language—ideal for Python learners. They also provide editorials and community support for deeper understanding.

























Did you enjoy this article?