Linked List in Data Structure: A Complete Guide

In data structures, linked lists stand as one of the fundamental building blocks, offering dynamic storage and efficient manipulation of data. Unlike arrays, linked lists provide flexibility in memory allocation and enable seamless insertion and deletion operations.

Understanding the anatomy and operations of linked lists is important for mastering data structure concepts and implementing efficient algorithms.

In this blog, we will explore linked lists, and learn their significance and operations. Let’s explore linked lists and learn why they remain important in computer science and software development.

What is a Linked List?

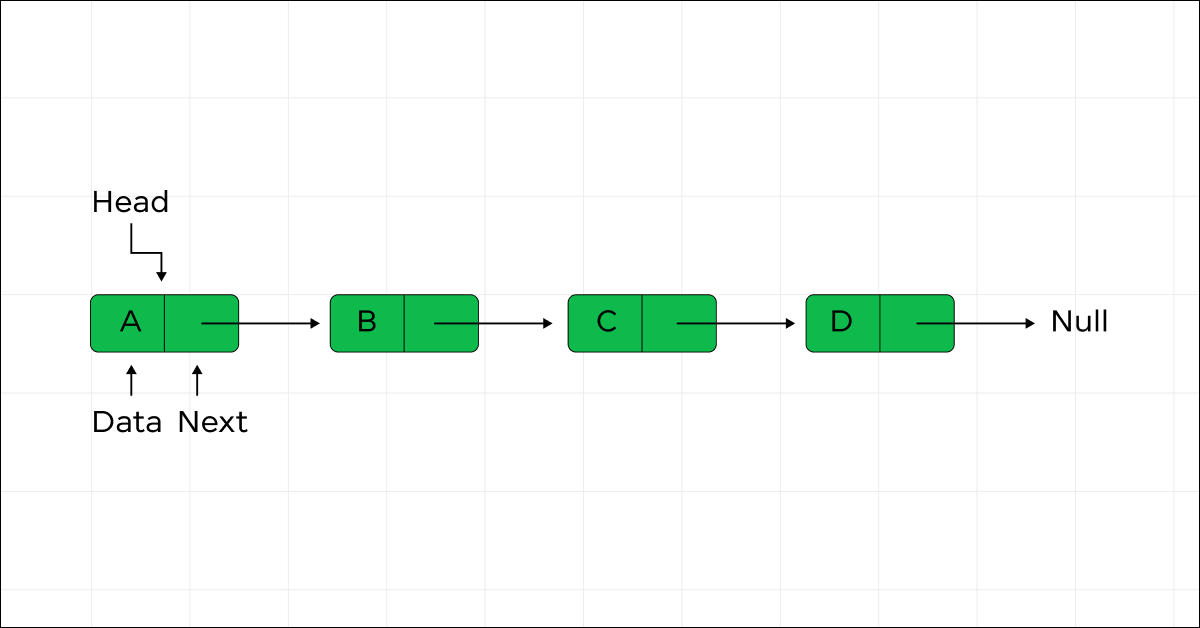
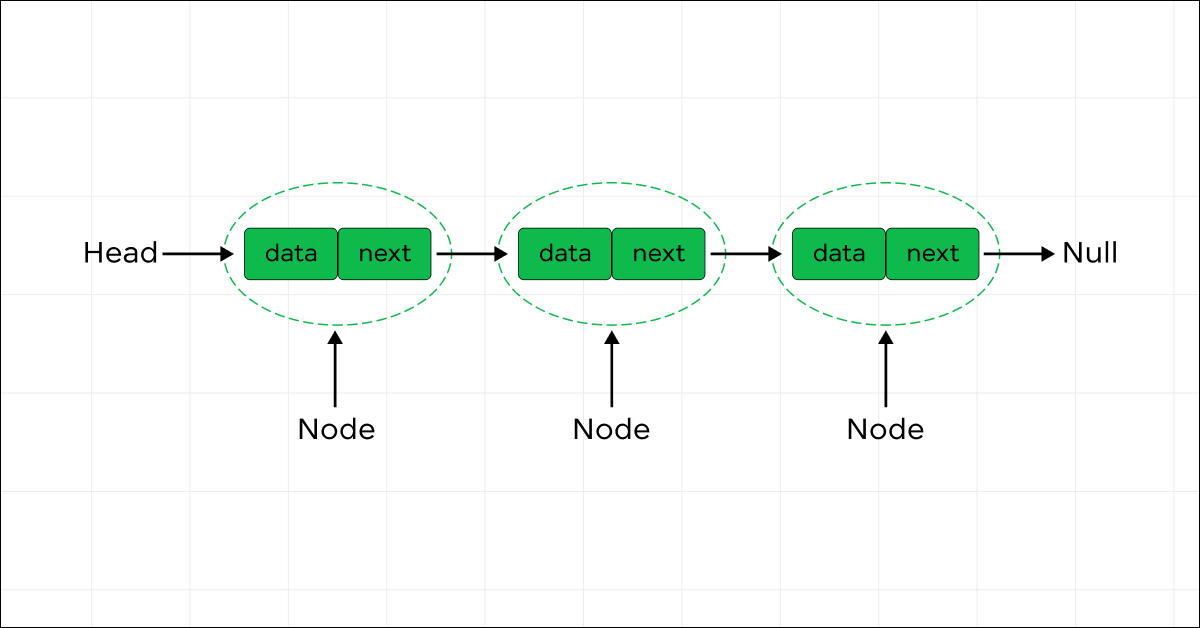
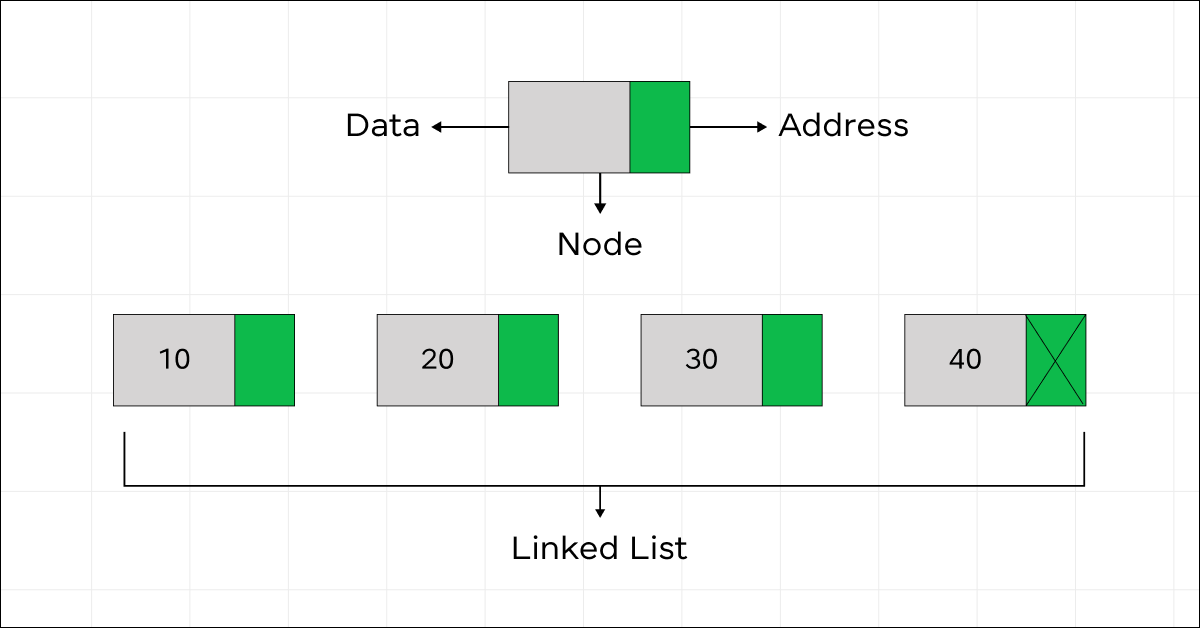
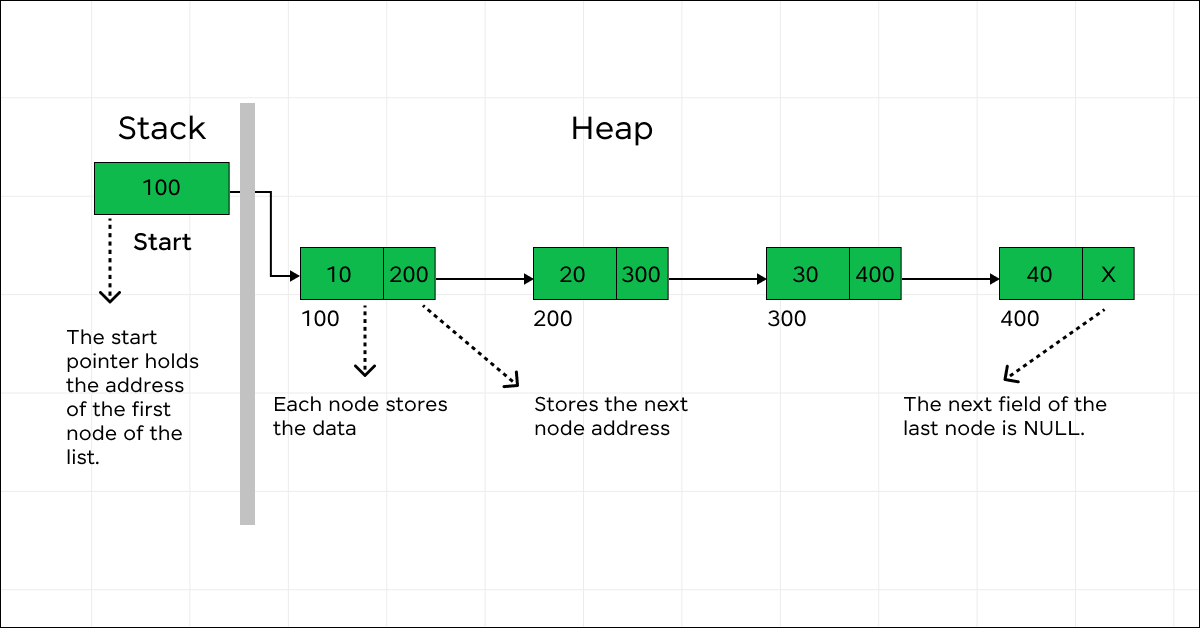
A linked list is a linear data structure in which the elements are not stored in contiguous memory locations. Instead, each element called a node, contains a data field and a reference (or link) to the next node in the sequence. The order of the nodes is determined by these links, rather than their physical memory locations.

The key components of a linked list are:

1. Node: Each node consists of two parts:

• Data: The actual data or value stored in the node.
• Next: A pointer or reference that points to the next node in the list.

2. Head: The head is a special pointer that points to the first node in the linked list. It serves as the entry point to access the list.

Nodes are dynamically allocated and linked together using pointers. The last node in the list typically has its “next” pointer set to null, indicating the end of the list.

Also Read: How to Start Competitive Programming in 5 Simple Steps?

Types of Linked Lists

There are several types of linked lists, each with its own characteristics and use cases. Let’s go through some common types:

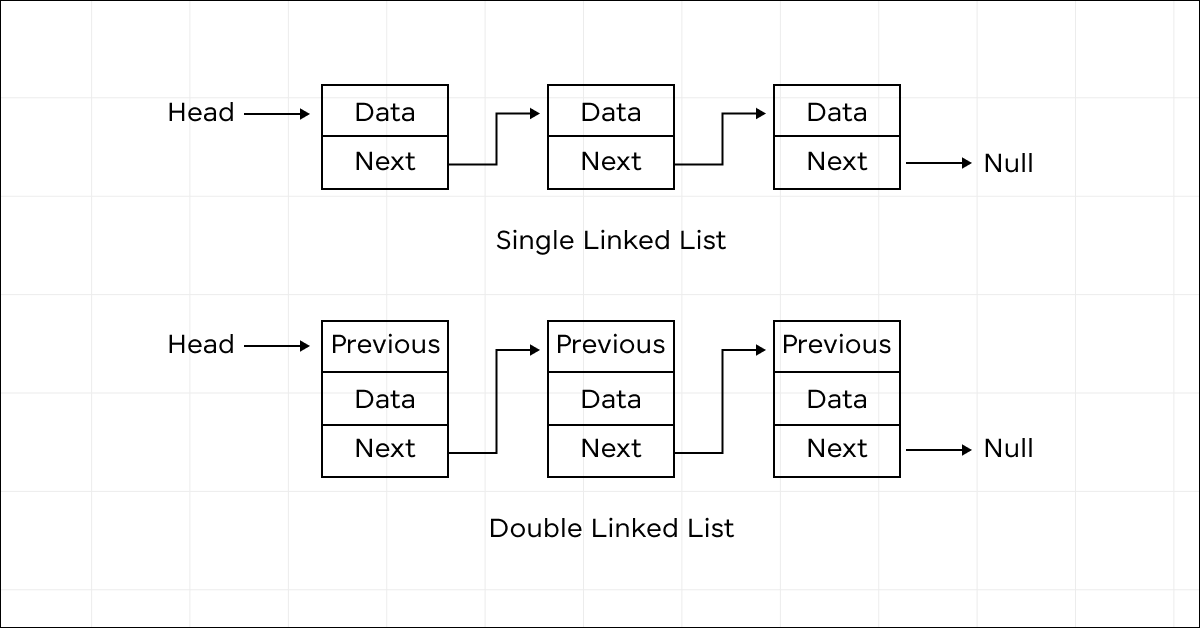
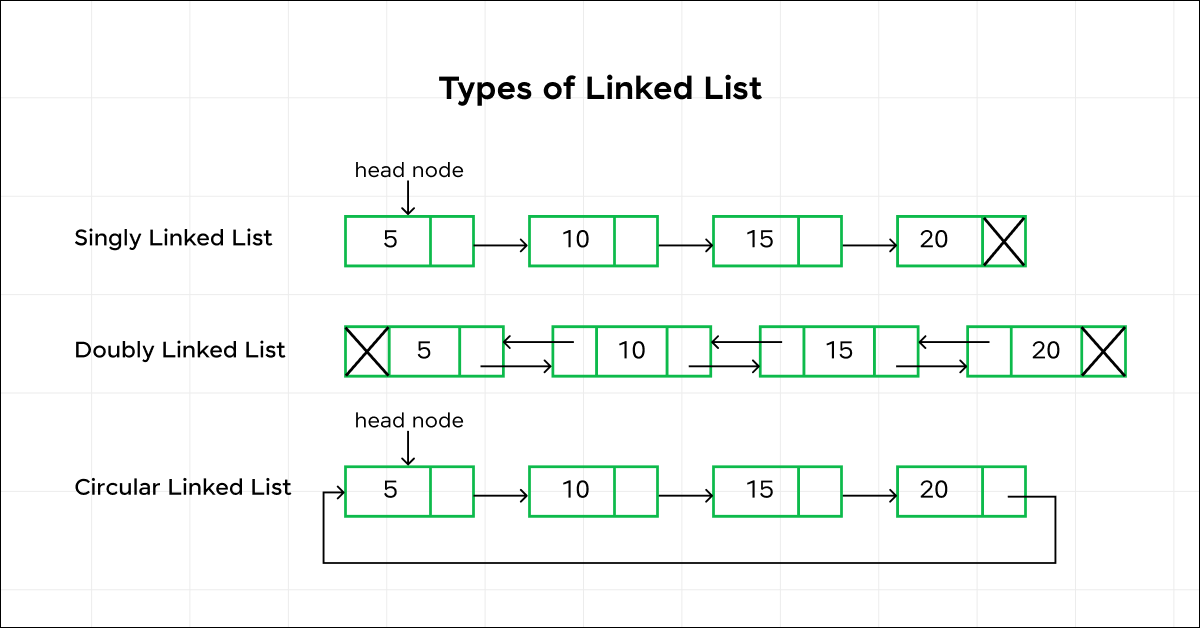
1. Singly Linked List: In this type of linked list, each element in the list is stored in a node that contains a reference to the next node in the sequence. The last node points to null.

Head -> Node1 -> Node2 -> Node3 -> ... -> NodeN -> null

2. Doubly Linked List: In a doubly linked list, each node contains references to both the next and the previous nodes in the sequence. This allows traversal in both forward and backward directions.

null <- Node1 <-> Node2 <-> Node3 <-> ... <-> NodeN -> null

3. Circular Linked List: In a circular linked list, the last node points back to the first node, forming a circular structure. This can be implemented with singly or doubly linked lists.

Head -> Node1 -> Node2 -> Node3 -> ... -> NodeN -> Head

4. Sorted Linked List: A sorted linked list maintains its elements in sorted order, typically ascending or descending. Insertion in a sorted list involves finding the correct position for the new element to maintain the order.

Head -> 1 -> 3 -> 5 -> 7 -> 9 -> null

Linked lists provide several advantages over arrays, such as dynamic memory allocation, efficient insertion and deletion operations, and flexible size. However, they lack efficient random access and have memory overhead due to the additional pointers required for each node.

Also, Find Out How much DSA for Full Stack Development Is Required?

Are you ready to elevate your expertise in full-stack development? Begin your transformative journey towards becoming a proficient full-stack developer by enrolling in GUVI’s Full Stack Development Course. Enroll now!

Now that we have an understanding of what a linked list is and how it functions, let’s explore the various operations that can be performed on linked lists to manipulate and manage the data they contain.

Operations on Linked Lists

Linked lists support several fundamental operations, each with its own time complexity. Here are some common operations and their time complexities:

1. Traversal: Accessing each element of the linked list sequentially. Time complexity: O(n), where n is the number of nodes in the list.

Start from the head and iterate through the list, printing each node’s data.

def traverse(self):
    current = self.head
    while current:
        print(current.data)
        current = current.next

Also Explore: 5 Best Reasons to Learn Data Structures and Algorithms [DSA]

2. Search: Finding a specific element in the linked list. Time complexity: O(n) in the average case, as it requires traversing the entire list in the worst case.

Start from the head and traverse the list, comparing each node’s data with the target value until finding a match or reaching the end of the list.

def search(self, target):
    current = self.head
    while current:
        if current.data == target:
            return True
        current = current.next
    return False

3. Insertion

a. Inserting at the beginning: Adding a new node at the start of the linked list. Time complexity: O(1), as it only requires updating the head pointer.
1. Create a new node.
2. Set its data.
3. Set its next pointer to the current head.
4. Update the head to point to the new node.

def insert_at_beginning(self, data):
    new_node = Node(data)
    new_node.next = self.head
    self.head = new_node

b. Inserting at the end: Adding a new node at the end of the linked list. Time complexity: O(1) for doubly linked lists, O(n) for singly linked lists, as you need to traverse to the end of the list.

1. Create a new node.
2. Set its data.
3. Traverse the list until reaching the last node.
4. Set the next pointer of the last node to the new node.

def insert_at_end(self, data):
    new_node = Node(data)
    current = self.head
    while current.next:
        current = current.next
    current.next = new_node

c. Inserting in the middle: Adding a new node at a specific position in the linked list. Time complexity: O(n), as you need to traverse to the desired position.

1. Create a new node.
2. Set its data.
3. Traverse the list until reaching the node before the desired position.
4. Adjust pointers to insert the new node.

def insert_at_position(self, position, data):
    new_node = Node(data)
    current = self.head
    for _ in range(position - 1):
        current = current.next
    new_node.next = current.next
    current.next = new_node

Also Read: 40 Java Interview Questions for Freshers with Clear & Concise Answers

4. Deletion

a. Deleting the head node: Removing the first node from the linked list. Time complexity: O(1), as it only requires updating the head pointer.

1. Update the head to point to the second node.
2. Free the memory of the deleted node.

def delete_at_beginning(self):
    if self.head:
        temp = self.head
        self.head = self.head.next
        del temp

b. Deleting the last node: Removing the last node from the linked list. Time complexity: O(n) for singly linked lists, as you need to traverse to the second-last node, and O(1) for doubly linked lists.

1. Traverse the list until reaching the second last node.
2. Update its next pointer to null.
3. Free the memory of the last node.

def delete_at_end(self):
    current = self.head
    if current:
        if not current.next:
            self.head = None
            return
        while current.next.next:
            current = current.next
        temp = current.next
        current.next = None
        del temp

c. Deleting a node in the middle: Removing a node at a specific position in the linked list. Time complexity: O(n), as you need to traverse to the desired position.

1. Traverse the list until reaching the node before the desired position.
2. Adjust pointers to skip the node to be deleted.
3. Free its memory.

def delete_at_position(self, position):
    if position == 0:
        self.delete_at_beginning()
        return
    current = self.head
    for _ in range(position - 1):
        current = current.next
    temp = current.next
    current.next = temp.next
    del temp

It’s important to note that these time complexities assume that you have a reference to the desired position in the linked list. If you need to find the desired position first, an additional O(n) traversal would be required, increasing the overall time complexity.

Additionally, some operations like inserting or deleting at the beginning or end of a doubly linked list can be performed in constant time, O(1), as both the head and tail pointers are maintained.

The time complexity of operations on linked lists is generally better for insertion and deletion compared to arrays, but worse for accessing elements by index or random access. The choice between using a linked list or an array depends on the specific requirements of the application and the operations that need to be performed frequently.

Also Read: Best DSA Roadmap Beginners Should Know 2024

Having explored the operations that can be performed on linked lists to manipulate data efficiently, let’s learn the applications of this data structure.

Applications of Linked Lists

Linked lists have numerous applications across various domains due to their flexibility, efficiency, and ease of implementation. Here are some common applications:

1. Dynamic Memory Allocation: Linked lists are often used in dynamic memory allocation systems, such as in programming languages like C and C++, to manage memory efficiently. They allow for the allocation and deallocation of memory blocks as needed.
2. Implementation of Stacks and Queues: Linked lists are fundamental in implementing abstract data types like stacks and queues. In a stack, elements are added and removed from the same end (last-in, first-out), while in a queue, elements are added at one end and removed from the other end (first-in, first-out).
3. Sparse Matrix Representation: Sparse matrices that contain mostly zero values can be efficiently represented using linked lists. Each node of the linked list represents a non-zero element along with its row and column indices.
4. Graphs: Linked lists can be used to represent graphs, a collection of nodes (vertices) connected by edges. Each node in the linked list represents a vertex, and its adjacency list contains references to the vertices it is connected to.
5. Symbol Tables: Linked lists are commonly used to implement symbol tables in compilers and interpreters. Each node in the linked list contains information about a symbol, such as its name, type, and value.
6. Polynomial Manipulation: Linked lists can be used to represent and manipulate polynomials efficiently. Each node in the linked list represents a term in the polynomial, with fields for the coefficient and exponent.
7. Music and Playlist Management: Linked lists can be used to implement playlists in music applications. Each node represents a song, with fields for metadata such as title, artist, and duration. Users can easily add, remove, or rearrange songs in the playlist.
8. Undo Functionality: Linked lists are useful for implementing undo functionality in text editors and other software applications. Each node in the linked list represents a state or action, allowing users to revert to previous states by traversing the list.
9. Navigation Systems: Linked lists can be used to represent routes and navigation paths in GPS and map applications. Each node in the linked list represents a location, and its adjacent nodes represent possible next destinations.
10. Job Scheduling: Linked lists are used in operating systems for job scheduling algorithms. Each node in the linked list represents a job or process, and the order of nodes determines the execution sequence.

These are just a few examples of the wide range of applications where linked lists are used. Their simplicity and versatility make them a valuable tool in computer science and software development.

Also, Explore About 10 Best Data Structures and Algorithms Courses [2024]

Linked lists are beneficial when you need dynamic data structures with efficient insertion and deletion operations, and when the size of the data structure is not known in advance. However, they may not be the best choice if you require frequent random access or if memory overhead is a significant concern.

The decision to use a linked list or another data structure depends on the specific requirements and trade-offs of your application.

Take the initiative to learn full stack development with GUVI’s Full Stack Development course, designed to provide you with expert guidance and hands-on learning experiences.

Conclusion

Linked lists remain an important part of data structure fundamentals, offering versatility and efficiency in managing data. Understanding their principles and applications equips us with valuable insights into data manipulation and lays the groundwork for tackling complex problems in software development and beyond.

Also Read: Is DSA Important for Placement in 2024?

FAQs

Why choose a linked list over an array?

Linked lists offer several advantages over arrays. Firstly, they provide dynamic memory allocation, allowing for efficient memory usage and flexibility in size adjustments.
Unlike arrays, which have a fixed size, linked lists can grow or shrink as needed, making them suitable for scenarios where the size of the data structure is unknown or may change over time.

What are the main types of linked lists?

Linked lists come in various types, each with its unique characteristics. The most common types include singly linked lists (each node contains data and a pointer to the next node in the sequence), doubly linked lists (extend this concept by including a pointer to the previous node as well, enabling traversal in both forward and backward directions), and circular linked lists (form a loop where the last node points back to the first node, creating a circular structure).

How do you perform basic linked list operations?

Basic operations on linked lists include insertion, deletion, and traversal:

1) Insertion involves creating a new node with the desired data and adjusting pointers to include it in the appropriate position within the list.
2) Deletion requires updating pointers to bypass the node to be removed, effectively removing it from the sequence.
3) Traversal entails sequentially moving through each node in the list, starting from the head or another designated starting point, and accessing or modifying data as needed.