
Binary Tree vs Binary Search Tree: Learn What Sets Them Apart!
Dec 12, 2025 10 Min Read 1724 Views
(Last Updated)
Have you ever wondered how computers organize data so efficiently that they can locate a value among millions in just a few microseconds? The answer lies in hierarchical structures like Binary Trees and Binary Search Trees (BSTs). These two models define how information is arranged, accessed, and modified in almost every core computing process, from database indexing to AI decision-making. A Binary Tree provides a flexible foundation for representing hierarchical relationships, whereas a Binary Search Tree refines this structure to support ordered and efficient searching.
To understand how these trees differ in architecture, performance, and real-world usage, read the complete blog for detailed explanations and practical insights.
Table of contents
- What is a Binary Tree?
- What is a Binary Search Tree?
- Basic Terminologies Used in a Binary Tree vs. Binary Search Tree
- Basic Terminologies Used in a Binary Tree
- Basic Terminologies Used in a Binary Search Tree
- Benefits of a Binary Tree vs. Binary Search Tree
- Advantages of a Binary Tree
- Advantages of Binary Search Tree
- Applications of a Binary Tree vs. Binary Search Tree
- Applications of a Binary Tree
- Applications of Binary Search Tree
- Disadvantages of a Binary Tree
- Disadvantages of a Binary Search Tree
- Step-by-Step Implementation of a Binary Tree
- Node Structure Definition
- Establishing the Root Node
- Node Insertion Process
- Traversal Techniques
- Searching for a Node
- Node Deletion
- Height and Balance Calculation
- Tree Traversal Termination
- Binary Tree Implementation (Python)
- Explanation
- Step-by-Step Implementation of a Binary Search Tree
- Node Definition
- Insertion Operation
- Search Operation
- Deletion Operation
- Traversal Methods
- Balancing (Optional Step)
- Binary Search Tree Implementation (Python)
- Explanation
- Binary Tree vs. Binary Search Tree
- Conclusion
- FAQs
- What is the main difference between a Binary Tree and a Binary Search Tree in DSA?
- Why is a Binary Search Tree preferred for database indexing?
- Which is better to use: Binary Tree or Binary Search Tree?
What is a Binary Tree?
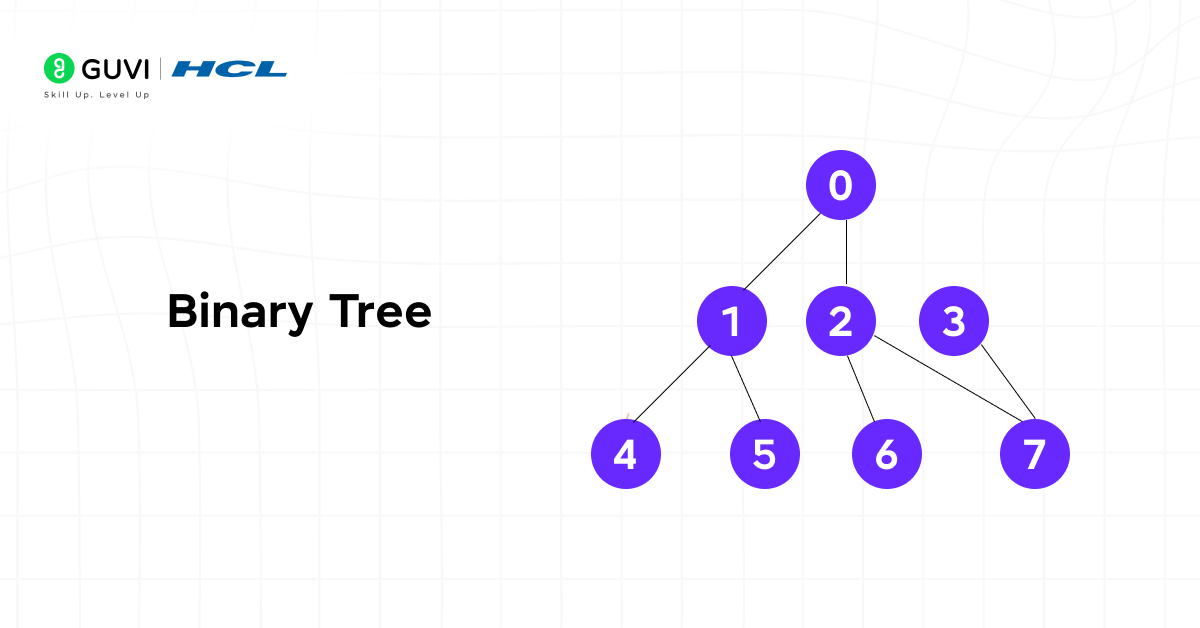
A Binary Tree is a structured data model that organizes elements in a hierarchical order where each node connects to at most two child nodes. This arrangement strengthens a connected structure with no cycles. Binary Trees are used widely in algorithm design because they balance storage efficiency with operational speed. Their recursive nature helps in solving hierarchical problems that require partitioning data into smaller substructures.
What is a Binary Search Tree?
A Binary Search Tree (BST) is a specialized form of a Binary Tree. It organizes data in a sorted hierarchical structure to support efficient search, insertion, and deletion operations. Binary Search Trees constitute the foundation for numerous data-intensive applications, including databases and operating systems. They provide a clear and logical framework for organizing data that supports both rapid access and structured relationships between elements.
Basic Terminologies Used in a Binary Tree vs. Binary Search Tree
Basic Terminologies Used in a Binary Tree

1. Node: A node represents an individual element of the Binary Tree. It contains three components: the data value, a pointer to the left child, and a pointer to the right child.
2. Root Node: The root node is the topmost element of the Binary Tree. It serves as the entry point for all operations and has no parent node.
3. Parent Node: A parent node is any node that has at least one child. It connects to its child nodes through left and right pointers.
4. Child Node: A child node is directly connected to a parent node. It can be either a left child or a right child, depending on its position relative to the parent.
5. Leaf Node: A leaf node is a terminal node that does not have any child nodes. It marks the endpoint of a branch in the tree.
6. Internal Node: An internal node has at least one child. It lies between the root and the leaf nodes and contributes to the tree’s branching structure.
7. Sibling Nodes: Sibling nodes share the same parent. They exist at the same level and connect through separate branches from a common parent node.
8. Edge: An edge is the connection or link between two nodes. It represents the relationship between a parent and its child.
9. Path: A path is the sequence of nodes and edges connecting one node to another. It helps determine traversal depth and connectivity.
10. Height of a Tree: The height of a Binary Tree is the length of the longest path from the root to any leaf node. It represents the overall depth of the tree structure.
11. Depth of a Node: The depth of a node measures how far that node is from the root. It counts the number of edges between the node and the root.
12. Level of a Node: The level of a node is its position relative to the root, where the root is at level 1 and its children are at level 2, and so on.
13. Subtree: A subtree is any node along with all its descendants. Each node in a Binary Tree can be considered the root of its own subtree.
Basic Terminologies Used in a Binary Search Tree

1. Binary Search Property: In a BST, each node follows an ordered rule:
- The left child holds a value smaller than the parent.
- The right child holds a value greater than the parent.
2. Key: The key represents the data stored in each node that determines its position in the tree based on comparison during insertion or search.
3. Root Node: The root node is the starting point of the BST. All insertions and searches begin from this node, following the binary search property.
4. Left Subtree: The left subtree contains all nodes with values smaller than the root. It maintains the same binary ordering rule recursively for all its descendants.
5. Right Subtree: The right subtree contains all nodes with values greater than the root. Each of its descendants also satisfies the BST property.
6. Balanced Tree: A balanced BST maintains nearly equal height on both sides of the root. This balance ensures efficient performance for search, insertion, and deletion operations.
7. Unbalanced Tree: An unbalanced BST has uneven height distribution, often forming a linear chain of nodes. It reduces efficiency and increases search time to linear complexity.
8. Successor and Predecessor: The successor of a node is the smallest value greater than the current node, usually found in its right subtree. The predecessor is the largest value smaller than the current node. It is generally found in its left subtree.
9. Minimum and Maximum Node: The minimum node in a BST is located at the leftmost position, and the maximum node is at the rightmost position.
10. Height of BST: The height of a Binary Search Tree is the number of edges on the longest path from the root to a leaf node. It affects search and insertion efficiency.
11. Traversal Orders: BSTs commonly use inorder, preorder, and postorder traversals. Inorder traversal yields sorted data because it processes nodes in ascending order based on their values.
Benefits of a Binary Tree vs. Binary Search Tree
Advantages of a Binary Tree

- Efficient Search and Ordered Data Handling
Binary Trees organize data in a hierarchical structure where each node can have up to two children: a left and a right child, without enforcing any specific ordering between their values. This ordering allows search, insertion, and deletion operations to complete in logarithmic time in balanced conditions. They reduce the need for full dataset scans, which improves computational efficiency for large datasets.
- Logical Representation of Hierarchical Relationships
A Binary Tree represents data that follows a natural hierarchy, such as family trees, directory structures, and expression parsing in programming languages. Each node represents a level of abstraction, which makes the structure suitable for interpreting nested or dependent relationships within data models.
- Foundational Structure for Advanced Algorithms
Many advanced data structures in DSA originate from Binary Trees. AVL Trees, Red-Black Trees, and Heaps are extensions that improve specific operations such as balancing, prioritization, and range computation. These derivatives build on the Binary Tree’s principle of ordered branching and structured recursion.
- Support for Recursive Computation
Recursive algorithms work effectively with Binary Trees because each node can be treated as the root of its own subtree. Traversals such as inorder, preorder, and postorder process data in specific sequences that support operations like sorting, syntax evaluation, and decision-making in computational processes.
- Controlled Memory Utilization
Binary Trees adapt well to varying input sizes through dynamic memory allocation. Each node is created independently and linked by pointers, which means memory expands or contracts according to data requirements. This feature benefits systems that manage changing data volumes or variable hierarchical depths.
Advantages of Binary Search Tree

1. Efficient Searching and Retrieval
A Binary Search Tree reduces the number of comparisons required to locate a specific value. Each traversal decision eliminates half of the remaining nodes. It authorizes search operations to execute in logarithmic time under balanced conditions. This structure improves data access speed compared to linear data structures such as arrays or linked lists.
2. Simplified Insertion and Deletion Operations
Insertion and deletion in a BST follow a consistent comparison-based pattern. The new value is placed in the correct position based on its relation to existing nodes, and removal adjusts pointers without disturbing the tree’s sorted structure. These operations preserve order while avoiding complete data rearrangement.
3. Automatic Data Ordering
A BST maintains data in a sorted state by design. Performing an inorder traversal returns all elements in ascending order, which removes the need for separate sorting algorithms. This property supports applications that require ordered iteration or range queries.
4. Scalable Storage Structure
The hierarchical layout of a BST adapts well to varying data sizes. Balanced trees such as AVL or Red-Black Trees maintain near-uniform height, which prevents performance degradation even as the dataset grows. This scalability makes BSTs suitable for real-time systems that handle expanding data volumes.
5. Foundation for Advanced Data Structures
The Binary Search Tree serves as the base for several advanced data structures such as Binary Heaps, Segment Trees, and B-Trees. These enhanced variants expand on the BST’s principles to support priority handling, interval queries, and efficient disk-based indexing. The conceptual clarity of BST operations provides a foundation for understanding complex algorithmic designs.
Applications of a Binary Tree vs. Binary Search Tree
Applications of a Binary Tree

- Binary Trees for Data Retrieval
A Binary Tree organizes data in a sorted format that supports quick access. Each comparison reduces the search space by half, leading to efficient lookups. Database management systems and in-memory data managers rely on this property to maintain speed and accuracy.
- Expression Evaluation and Compiler Design
Binary Trees are used to build expression trees in compilers. Operators serve as internal nodes, and operands appear as leaf nodes. Recursive traversal of these trees helps evaluate complex arithmetic expressions and optimize computation sequences.
- Data Compression through Huffman Coding
Huffman Trees are special Binary Trees that represent symbols based on their frequency. Characters with higher occurrence get shorter binary codes. This method is used in file compression systems and image storage formats to reduce file size without losing data.
- Priority-Based Processing in Heaps
Heaps, a form of Binary Tree, store elements based on priority rather than value order. They are used in task scheduling, memory allocation, and algorithms such as Dijkstra’s shortest path. Their structured shape keeps insertion and extraction operations efficient even for large datasets.
- Decision-Making and Classification in AI
Binary Trees form the structure of decision trees used in machine learning models. Each internal node performs a condition check, and each branch represents an outcome. This method supports regression and logical rule-based reasoning in systems that interpret real-world data.
Applications of Binary Search Tree

1. Searching and Indexing in DatabasesSearching and Indexing in Databases
In DSA, Binary Search Trees are widely used in database indexing systems to organize and retrieve records efficiently. Their hierarchical structure supports range queries and ordered traversals, which makes them integral to indexing mechanisms such as B-Trees and B+ Trees. This structure ensures that large volumes of data can be accessed, inserted, and updated with logarithmic efficiency, which strengthens database performance under dynamic workloads.
2. Symbol Tables in Compilers
Compilers use BSTs to manage identifiers and variable scopes through symbol tables. The tree structure provides quick insertion, lookup, and deletion of symbols during compilation, improving both speed and memory management in lexical and semantic analysis.
3. Data Compression and Encoding
BSTs play a critical role in encoding algorithms like Huffman coding. The tree structure enables efficient assignment of variable-length binary codes based on frequency, which reduces redundancy and optimizes data compression.
4. File Systems and Memory Allocation
File systems and memory managers apply BST principles to track file metadata and allocate memory blocks. The ordered structure assists in locating available space or recently used blocks with minimal traversal overhead.
5. Autocomplete and Search Optimization
BSTs are applied in text editors, search engines, and user interface design for real-time suggestions. They permit efficient prefix-based lookups by maintaining ordered word sequences. It basically speeds up predictive typing and search optimization.
Disadvantages of a Binary Tree
- An unbalanced Binary Tree may degrade search performance to linear time.
- Extra memory is required for storing references to child nodes.
- Insertion and deletion operations are complex in maintaining tree balance.
- Traversals often depend on recursion, which increases function call overhead.
- Sequential access of data is slower than array-based structures.
Disadvantages of a Binary Search Tree
- Performance depends heavily on tree balance. An unbalanced tree behaves like a linked list and increases search time to linear complexity.
- Recursion in traversal and insertion can consume significant stack memory for large datasets.
- Deletion requires multiple comparisons and pointer adjustments, which increases implementation complexity.
- Frequent insertions and deletions can lead to imbalance unless self-balancing mechanisms are applied.
- Maintaining sorted order in dynamic datasets can result in additional computational overhead.
Step-by-Step Implementation of a Binary Tree
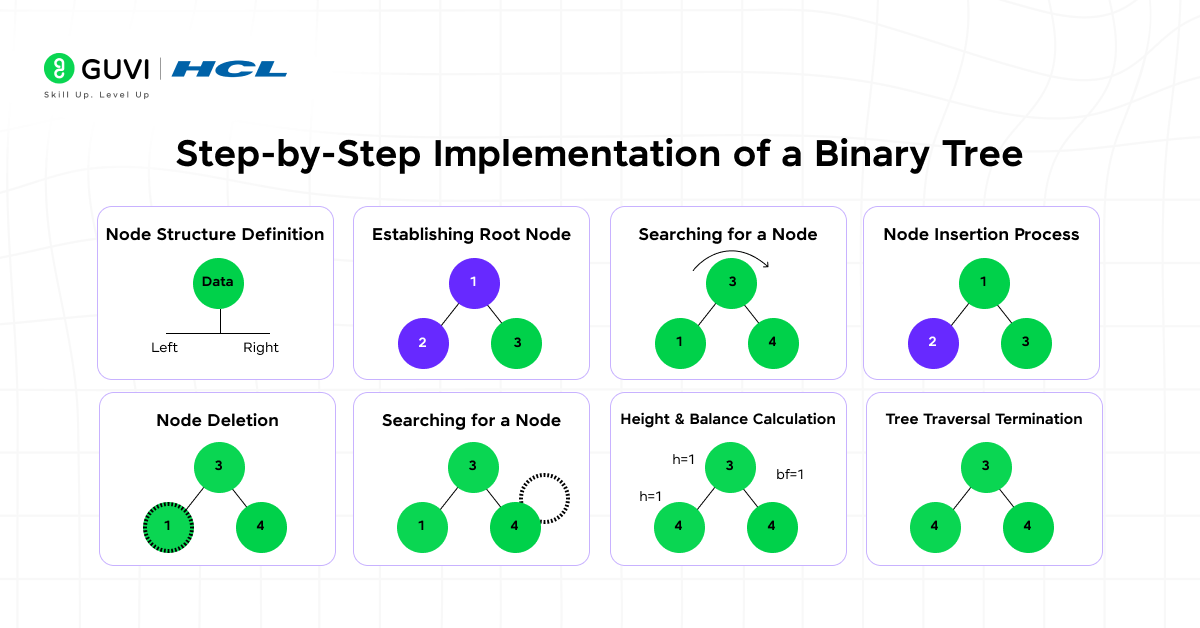
1. Node Structure Definition
A Binary Tree is composed of nodes, and each node stores data along with links to its left and right children. The root node acts as the entry point, and every other node connects downward to form subtrees. Each connection represents a parent-child relationship, which establishes the hierarchical structure.
2. Establishing the Root Node
The construction begins by creating the root node. It is the topmost node and has no parent. The root defines the starting point for all operations, such as insertion, traversal, or deletion. Every subsequent node is positioned based on its relationship to the root.
3. Node Insertion Process
Insertion adds new nodes to the tree while maintaining its hierarchical integrity.
- Identify the correct position for the new node under an existing parent.
- Attach the node as a left or right child based on the available link.
- Repeat the process for additional nodes to expand the structure.
This step ensures that the tree remains connected and accessible from the root.
4. Traversal Techniques
Traversal refers to visiting every node in a specific sequence.
- Inorder Traversal (Left → Root → Right): Produces data in sorted order if applied to a Binary Search Tree.
- Preorder Traversal (Root → Left → Right): Useful for copying or serializing the tree.
- Postorder Traversal (Left → Right → Root): Commonly used in deleting or evaluating expressions.
Each traversal follows a systematic path to process every node exactly once.
5. Searching for a Node
Searching in a Binary Tree checks whether a specific value exists within the structure. The algorithm begins at the root and explores each subtree recursively or iteratively. The search continues until the desired value is located or all paths have been examined.
6. Node Deletion
Deletion modifies the tree by removing a selected node.
- If the node is a leaf, it is simply detached.
- If the node has one child, the child replaces it directly.
- If the node has two children, a suitable replacement (such as an inorder successor) is chosen to maintain the structure.
After deletion, the links are updated to keep the tree connected.
7. Height and Balance Calculation
The height of a Binary Tree is the length of the longest path from the root to any leaf. Maintaining balance helps optimize traversal and search performance. Some variants, such as AVL Trees, adjust node placement automatically to control height differences.
8. Tree Traversal Termination
The implementation completes when all nodes have been inserted, connected, and verified through traversal. A properly constructed Binary Tree maintains accessible pathways from the root to every node and supports reliable operations such as search and deletion.
Binary Tree Implementation (Python)
Sample Code:
# Define a class for a node in the binary tree
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
# Define the Binary Tree class
class BinaryTree:
def __init__(self):
self.root = None
# Insert nodes level-wise
def insert(self, value):
new_node = Node(value)
if not self.root:
self.root = new_node
return
queue = [self.root]
while queue:
current = queue.pop(0)
if not current.left:
current.left = new_node
return
else:
queue.append(current.left)
if not current.right:
current.right = new_node
return
else:
queue.append(current.right)
# Inorder Traversal: Left → Root → Right
def inorder(self, node):
if node:
self.inorder(node.left)
print(node.value, end=" ")
self.inorder(node.right)
# Preorder Traversal: Root → Left → Right
def preorder(self, node):
if node:
print(node.value, end=" ")
self.preorder(node.left)
self.preorder(node.right)
# Postorder Traversal: Left → Right → Root
def postorder(self, node):
if node:
self.postorder(node.left)
self.postorder(node.right)
print(node.value, end=" ")
# Create Binary Tree and insert elements
tree = BinaryTree()
elements = [10, 20, 30, 40, 50, 60, 70]
for e in elements:
tree.insert(e)
# Display traversals
print("Inorder Traversal:")
tree.inorder(tree.root)
print("\nPreorder Traversal:")
tree.preorder(tree.root)
print("\nPostorder Traversal:")
tree.postorder(tree.root)
Expected Outcome:
Inorder Traversal:
40 20 50 10 60 30 70
Preorder Traversal:
10 20 40 50 30 60 70
Postorder Traversal:
40 50 20 60 70 30 10
Explanation
- Insertion: Nodes are inserted level by level (top to bottom, left to right).
- Inorder Traversal: Visits nodes in sorted logical order for certain tree types.
- Preorder Traversal: Visits parent nodes before their children.
- Postorder Traversal: Visits all children before the parent node.
Also, explore: 10 Best Data Structures and Algorithms Courses [2025]
Want to build real AI-powered applications, not just models? Join our AI Software Development Course and learn how to integrate, deploy, and scale AI systems end-to-end. From API design to model serving, you’ll work on real projects under expert guidance, turning theory into practical, production-ready skills. Enroll now and start building the AI apps of tomorrow!
Step-by-Step Implementation of a Binary Search Tree
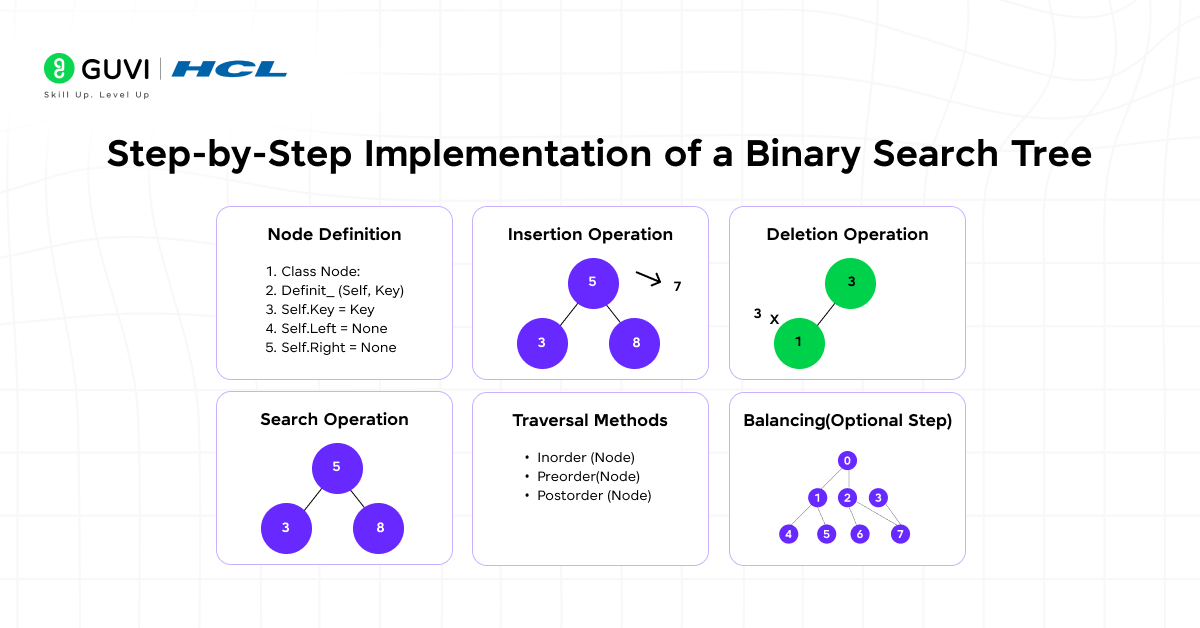
1. Node Definition
Each node in a Binary Search Tree contains three components:
- A data field to store the key or value
- A pointer to the left child node
- A pointer to the right child node
In most programming languages, this is implemented as a class or structure that defines these three attributes.
2. Insertion Operation
Insertion begins at the root node.
- Compare the value to be inserted with the current node.
- If the value is smaller, move to the left subtree.
- If the value is larger, move to the right subtree.
- Repeat until an empty position is found and insert the new node there.
This comparison process maintains the binary search property throughout the tree.
3. Search Operation
Searching follows the same logic as insertion.
- Start from the root and compare the target value with the current node.
- Move left if the target is smaller or right if it is larger.
- Continue until the value is found or the traversal reaches a null reference.
The process eliminates half of the remaining elements at each comparison, which allows efficient lookups.
4. Deletion Operation
Deletion depends on the node type:
- Leaf Node: Remove the node directly.
- Node with One Child: Replace the node with its child.
- Node with Two Children: Find the inorder successor or predecessor, replace the node’s value, and delete the duplicate from the subtree.
This maintains the BST’s order after deletion.
5. Traversal Methods
Traversal allows visiting all nodes systematically.
- Inorder Traversal: Left → Root → Right (produces sorted order)
- Preorder Traversal: Root → Left → Right
- Postorder Traversal: Left → Right → Root
These methods help analyze, print, or modify tree contents efficiently.
6. Balancing (Optional Step)
In cases where the tree becomes unbalanced, self-balancing variants such as AVL or Red-Black Trees can be used. They perform automatic rotations to strengthen logarithmic height and consistent performance.
Binary Search Tree Implementation (Python)
Sample Code:
# Define a class for a node in the Binary Search Tree
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
# Define the Binary Search Tree class
class BinarySearchTree:
def __init__(self):
self.root = None
# Insert a node into the BST
def insert(self, value):
if self.root is None:
self.root = Node(value)
return
current = self.root
while True:
if value < current.value:
if current.left is None:
current.left = Node(value)
return
current = current.left
elif value > current.value:
if current.right is None:
current.right = Node(value)
return
current = current.right
else:
# Ignore duplicate values
return
# Inorder Traversal: Left → Root → Right
def inorder(self, node):
if node:
self.inorder(node.left)
print(node.value, end=" ")
self.inorder(node.right)
# Preorder Traversal: Root → Left → Right
def preorder(self, node):
if node:
print(node.value, end=" ")
self.preorder(node.left)
self.preorder(node.right)
# Postorder Traversal: Left → Right → Root
def postorder(self, node):
if node:
self.postorder(node.left)
self.postorder(node.right)
print(node.value, end=" ")
# Create BST and insert elements
bst = BinarySearchTree()
elements = [50, 30, 70, 20, 40, 60, 80]
for e in elements:
bst.insert(e)
# Display traversals
print("Inorder Traversal:")
bst.inorder(bst.root)
print("\nPreorder Traversal:")
bst.preorder(bst.root)
print("\nPostorder Traversal:")
bst.postorder(bst.root)
Expected Output
Inorder Traversal:
20 30 40 50 60 70 80
Preorder Traversal:
50 30 20 40 70 60 80
Postorder Traversal:
20 40 30 60 80 70 50
Explanation
- Insertion: Each new node is placed based on the BST property.
- Values smaller than the parent go to the left subtree.
- Values larger than the parent go to the right subtree.
- Inorder Traversal: Produces data in ascending order, a key feature of BSTs.
- Preorder Traversal: Useful for creating a copy or visualizing tree hierarchy.
- Postorder Traversal: Often applied when deleting nodes or freeing memory.
Binary Tree vs. Binary Search Tree

Understanding the construction and internal logic of a binary tree and binary search tree builds a strong foundation for mastering Data Structures and Algorithms. Here are key differences between them:
| Factor | Binary Tree | Binary Search Tree (BST) |
| Definition | A hierarchical structure where each node has at most two children: left and right. | A structured Binary Tree where left child values are smaller and right child values are larger than the parent node. |
| Data Organization | Data is stored without a strict ordering rule. | Data follows a sorted hierarchical arrangement based on comparison. |
| Searching Efficiency | Searching may require traversal of all nodes, leading to O(n) time complexity. | Searching operates in O(log n) time for balanced trees because each comparison halves the search space. |
| Insertion Logic | New nodes can be placed at any available position. | New nodes are inserted according to the binary search property, maintaining sorted order. |
| Traversal Output (Inorder) | In-order traversal always produces data in ascending order. | It may consume more memory if the structure becomes uneven or sparse. |
| Duplication Handling | Duplicate values are allowed unless explicitly restricted. | Duplicate values are usually avoided or handled using defined insertion rules. |
| Structure Flexibility | Offers more flexibility in shape and node placement. | Maintains a defined structural order that influences placement and balance. |
| Memory Utilization | Expression parsing, hierarchical representation, Huffman coding, and decision trees. | Optimized memory use in balanced variants due to predictable node placement. |
| Use Cases | Expression parsing, hierarchical representation, Huffman coding, decision trees. | Search indexing, database indexing, symbol tables, and sorted data retrieval. |
| Performance Dependence | Performance depends on traversal type and implementation. | Performance depends on maintaining balance; unbalanced BSTs degrade to linear complexity. |
Want to master how Binary Trees and Binary Search Trees power efficient data storage and retrieval? Build and visualize these structures from scratch in our Data Structures & Algorithms using Java Course. Learn to implement traversals, optimize searches, and balance trees like a pro, all with real-world coding practice. Strengthen your foundation in DSA and prepare for top coding interviews with expert-led guidance.
Conclusion
Understanding the difference between a Binary Tree and a Binary Search Tree builds a strong conceptual base for mastering algorithms within any DSA roadmap. Both structures contribute to efficient data organization, rapid retrieval, and scalable storage across real-world applications. A Binary Tree provides flexibility for hierarchical data modeling, whereas a Binary Search Tree introduces order and precision that optimize performance for complex computational systems.
FAQs
1. What is the main difference between a Binary Tree and a Binary Search Tree in DSA?
A Binary Tree is a general hierarchical structure where each node can have up to two children, and there is no specific order for storing values. A Binary Search Tree (BST), on the other hand, maintains an ordered structure where left child nodes hold smaller values and right child nodes hold larger values.
2. Why is a Binary Search Tree preferred for database indexing?
In DSA, Binary Search Trees are fundamental to database indexing systems because they support quick searches, range queries, and ordered data retrieval. Variants like B-Trees and B+ Trees, derived from BST principles, maintain balanced structures that ensure logarithmic-time access even for massive datasets, which makes them ideal for databases and file systems.
3. Which is better to use: Binary Tree or Binary Search Tree?
The choice depends on the application. A Binary Tree is suitable for representing hierarchical data such as expression trees or decision trees. A Binary Search Tree is more efficient for applications that require frequent searching, insertion, and sorting, such as database indexing or compiler design in DSA projects.

























Did you enjoy this article?