
Logistic Regression in Machine Learning: A Complete Guide
Aug 29, 2025 6 Min Read 10926 Views
(Last Updated)
Ever wondered how your inbox automatically separates spam from real emails, or how banks instantly decide whether you’re eligible for a loan? That’s logistic regression quietly doing its job behind the scenes.
Despite being one of the oldest algorithms in machine learning, logistic regression remains a go-to solution for solving binary classification problems. It’s fast, interpretable, and surprisingly powerful in the right context.
In this article, you’ll get a detailed yet simple breakdown of how logistic regression works, why it’s different from linear regression, and what makes it so effective in real-world applications.
Table of contents
- What is Logistic Regression?
- Why Not Just Use Linear Regression?
- Problem 1: Output Range Is Unbounded
- Problem 2: No Natural Thresholding
- Problem 3: Poor Fit for Classification Metrics
- The Logistic Function (a.k.a. Sigmoid Function)
- What the Sigmoid Function Does:
- How Does Logistic Regression Work?
- Example:
- What this means:
- Training the Model: Cost Function and Gradient Descent
- The Cost Function: Log Loss (a.k.a. Binary Cross-Entropy)
- The Optimizer: Gradient Descent
- Learning Rate:
- Real-Life Examples of Logistic Regression
- Healthcare
- Finance
- Marketing
- Email Filtering
- Hiring and Admissions
- Evaluation Metrics for Logistic Regression
- Accuracy
- Precision and Recall
- F1 Score
- ROC Curve and AUC (Area Under the Curve)
- Logistic vs. Linear Regression: Key Differences
- Did You Know?
- When Should You Use Logistic Regression?
- Conclusion
- FAQs
- What is logistic regression used for in machine learning?
- What is the difference between logistic and linear regression?
- Why do we use the sigmoid function in logistic regression?
- Is logistic regression a linear model?
- When should I not use logistic regression?
What is Logistic Regression?

Logistic Regression is a supervised machine learning algorithm primarily used for binary classification tasks. That means it helps answer questions like:
- Is this email spam or not?
- Will this customer buy the product or not?
- Does this patient have the disease or not?
Despite the name, logistic regression isn’t used for regression problems (like predicting continuous values). Instead, it predicts the probability of an input belonging to a particular class. Once it has this probability, it applies a threshold (typically 0.5) to decide which class the input belongs to.
For example:
- If the model says there’s a 92% chance a student will pass, and our threshold is 0.5, we classify it as “pass”.
- If it’s 43%, we classify it as “fail”.
Key Characteristics:
- The output is a value between 0 and 1 (representing probability).
- It uses a sigmoid function to transform the raw model output into a probability.
- Often used as a baseline model because of its simplicity and interpretability.
So even though it’s simpler than modern deep learning models, logistic regression remains one of the most reliable tools for quick, clean classification.
Why Not Just Use Linear Regression?

On the surface, linear regression might look like it could do the job for classification. After all, it can also find relationships between input features and a target. But here’s the thing: it’s not built for classification tasks.
Let’s break down why it doesn’t work well for binary outcomes.
Problem 1: Output Range Is Unbounded
Linear regression predicts any real number; it can go from negative infinity to positive infinity. But for a classification task, we need the output to represent a probability, which should always be between 0 and 1.
Imagine your linear model predicts 3.7 or -1.2 for a class label. What does that even mean in probability terms? It doesn’t make sense.
Problem 2: No Natural Thresholding
Classification involves deciding between classes, and to do that, we need a clear decision boundary. Linear regression doesn’t give you a mechanism for that. Sure, you could manually say “if the output is above 0.5, it’s class 1,” but that doesn’t fix the range problem we just discussed.
Problem 3: Poor Fit for Classification Metrics
- Linear regression optimizes for Mean Squared Error (MSE), which assumes a continuous output.
- Classification tasks typically use log loss or cross-entropy, which are better suited for probability outputs.
In short, using linear regression for classification is like trying to cut vegetables with a spoon. It might work, but it’s not the right tool for the job.
The Logistic Function (a.k.a. Sigmoid Function)
This is the function that transforms the raw prediction of logistic regression into a probability score. It’s what makes logistic regression ideal for classification.
Here’s the sigmoid function:
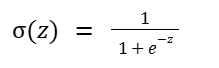
Where:
- z is the linear combination of weights and features:
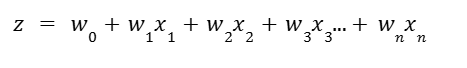
- e is the base of the natural logarithm (~2.718)
What the Sigmoid Function Does:
- It takes any real number as input.
- It squashes the output to lie between 0 and 1.
- It outputs a value that can be interpreted as a probability.
For example:
- If z = 0, then (z) = 0.5
- If z = 2, then (z) ≈ 0.88
- If z = -3, then (z) ≈ 0.047
This non-linearity is crucial. It allows the model to express confidence; values close to 0 or 1 mean the model is more certain, and values near 0.5 indicate uncertainty.
In summary, the sigmoid function is the bridge between raw linear predictions and meaningful probabilities. It’s what enables logistic regression to say, “Hey, based on this input, there’s an 82% chance of class 1, go with that.”
How Does Logistic Regression Work?

At a high level, logistic regression is about estimating the probability that a given input belongs to a particular class (like spam or not spam). It does this by combining linear algebra with probability theory.
Let’s go step-by-step to understand what happens behind the scenes when logistic regression makes a prediction:
It starts with a linear equation
Each input feature X is multiplied by a corresponding weight W, and a bias term B is added:
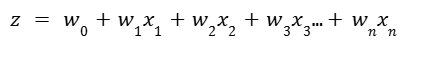
This result (z) is fed into a sigmoid function
The sigmoid squashes the value into a range between 0 and 1, turning it into a probability:
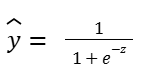
The model then applies a decision threshold
Typically, if it is greater than or equal to 0.5, the prediction is Class 1. If it’s less than 0.5, it’s Class 0.
Example:
Suppose you’re trying to predict whether a student will pass an exam based on hours of study.
- Input: 8 hours
- Model equation: z =−3 + 0.7⋅8 = 2.6
- Probability: y =(0.26) ≈ 0.93
- Interpretation: 93% chance they’ll pass → predicted class = 1
What this means:
The more hours a student studies, the higher the value of z, and thus the higher the predicted probability. Logistic regression draws a clean boundary between “likely to fail” and “likely to pass.”
Training the Model: Cost Function and Gradient Descent
Now you know how logistic regression predicts, but how does it learn in the first place?
The model starts with random weights and bias. During training, it updates these values so the predictions get closer to reality. This is where the cost function and gradient descent come in.
The Cost Function: Log Loss (a.k.a. Binary Cross-Entropy)
This function measures how far off the predicted probabilities are from the actual class labels. It penalizes confident wrong answers more than uncertain ones.

Key insights:
- If the actual class is 1, and the model says 0.99 → Low loss (good prediction).
- If the actual class is 1, and the model says 0.01 → High loss (bad prediction).
We calculate this loss for all training examples and try to minimize the average loss across the dataset.
The Optimizer: Gradient Descent
To minimize the cost, logistic regression uses gradient descent. Think of this like trying to find the lowest point in a valley (the minimum of the loss function).
Here’s how it works:
- Compute the gradient (i.e., slope) of the cost function for each weight.
- Adjust the weights in the opposite direction of the gradient.
- Repeat until the loss stops decreasing significantly.
Why this works:
- It’s a slow, steady improvement.
- Eventually, the weights settle at values where the predictions are as accurate as possible.
Learning Rate:
This controls how big each step is during gradient descent.
- Too high → You overshoot and never converge.
- Too low → You take forever to reach the bottom.
So, training logistic regression is a loop of:
→ Predict → Calculate Loss → Adjust Weights → Repeat
Real-Life Examples of Logistic Regression

You might think logistic regression is too basic to be useful in today’s world of AI and deep learning. But in reality, it’s used everywhere, especially in industries that need fast, interpretable models.
1. Healthcare
- Disease diagnosis: Predicting if a patient has diabetes, heart disease, or cancer based on clinical indicators.
2. Finance
- Credit scoring: Will a person default on a loan or not?
- Fraud detection: Is this transaction suspicious?
3. Marketing
- Click-through prediction: Will a user click on this ad?
- Churn prediction: Is a customer about to leave the platform?
4. Email Filtering
- Spam vs non-spam: Based on features like the presence of certain words, sender address, and email structure.
5. Hiring and Admissions
- Predicting success rates based on qualifications.
- For instance, HR teams can use logistic regression to predict if a candidate will accept a job offer or perform well based on past data.
Evaluation Metrics for Logistic Regression
Once your logistic regression model is trained, the next big question is: How well is it performing? For classification tasks, especially binary ones, accuracy isn’t the only thing you should be looking at. Let’s walk through the key metrics that matter.
1. Accuracy
This is the simplest metric: the percentage of predictions the model got right.
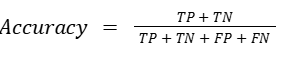
Where:
- TP = True Positives
- TN = True Negatives
- FP = False Positives
- FN = False Negatives
While accuracy is great for balanced datasets, it can be misleading when one class dominates the other. For example, if 95% of your emails are non-spam, a model that always predicts “non-spam” will be 95% accurate — but it’s useless.
2. Precision and Recall
These are more helpful when you’re dealing with imbalanced datasets (like fraud detection, disease diagnosis, etc.)
Precision: Of all the predicted positives, how many were positive?
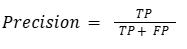
Recall: Of all the actual positives, how many did the model catch?
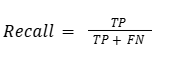
If your model says someone has cancer, you better be sure (high precision). But you also want to make sure you’re catching all actual cases (high recall).
3. F1 Score
This combines precision and recall into one single metric — the harmonic mean of the two.
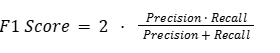
Why harmonic mean? Because it punishes extreme imbalances between precision and recall.
4. ROC Curve and AUC (Area Under the Curve)
The ROC curve plots the True Positive Rate (Recall) against the False Positive Rate at various threshold settings.
- A model that perfectly distinguishes between classes will have an AUC of 1.
- A model that performs no better than random guessing will have an AUC of 0.5.
AUC is especially useful when you want to evaluate performance across all classification thresholds, not just the default 0.5.
Logistic vs. Linear Regression: Key Differences

While they may sound similar, logistic and linear regression serve very different purposes and function in very different ways. Here’s how they compare:
| Aspect | Linear Regression | Logistic Regression |
| Problem Type | Used for regression problems where the goal is to predict a continuous value. For example, predicting salary, temperature, or sales volume. | Used for classification problems, especially binary classification. It’s ideal for predicting whether something belongs to class 0 or class 1 (e.g., spam or not). |
| Output Range | The model can output any real number between − to +, which is fine for numeric predictions but unsuitable for probabilities. | The output is always a value between 0 and 1, making it perfect for representing probabilities or likelihood of belonging to a class. |
| Prediction Target | Uses Log Loss (Binary Cross-Entropy), which heavily penalizes confident incorrect predictions, making it more suitable for classification. | Targets are categorical labels, either 0 or 1 in binary cases. The model tries to correctly classify the input using predicted probabilities. |
| Activation Function | No activation function is used. The output is just the linear combination of inputs and weights, like fitting a best-fit line through data. | Uses the sigmoid function (a.k.a. logistic function) to squash the output into a probability between 0 and 1. |
| Cost Function | Uses Mean Squared Error (MSE) to penalize large deviations between the predicted value and the actual output. | Uses Log Loss (Binary Cross-Entropy) which heavily penalizes confident incorrect predictions, making it more suitable for classification. |
| Interpretation | The output value is the predicted number itself. For example, 42.3 could mean ₹42.3K in predicted revenue. | The output is the probability of the input belonging to Class 1. For instance, 0.83 means an 83% chance of the input being a positive case. |
| Use Case Examples | Great for forecasting — like estimating stock prices, predicting product demand, or energy usage. | Used for decisions like credit approval, email spam filtering, disease detection, and customer churn prediction. |
Did You Know?
The name “logistic regression” comes from the logistic function, which is another name for the sigmoid function. It has nothing to do with logistics or supply chains.
Logistic regression was one of the earliest models used in the field of epidemiology to predict disease outcomes based on various risk factors.
When Should You Use Logistic Regression?
Use it when:
- You want a fast, interpretable model.
- The problem is binary classification.
- You want a strong baseline before testing heavier models.
- Your dataset isn’t massive or highly non-linear.
Don’t use it when:
- You have complex non-linear relationships (try Decision Trees or Neural Nets instead).
- You need a model that works out of the box on imbalanced data without tuning.
If you want to learn more about how Logistic Regression works in machine learning and how it can boost your learning, consider enrolling in GUVI’s IITM Pravartak Certified Artificial Intelligence and Machine Learning course that teaches NLP, Cloud technologies, Deep learning, and much more that you can learn directly from industry experts.
Conclusion
In conclusion, logistic regression may not be flashy like neural networks or as complex as ensemble models, but it earns its place in the machine learning hall of fame through sheer reliability and clarity.
The more you understand its inner workings, like the role of the sigmoid function, gradient descent, and log loss, the better you’ll be at applying it in the real world. A
nd now that you know everything about it, you’re in a great spot to not just use logistic regression, but actually trust what it’s telling you.
FAQs
1. What is logistic regression used for in machine learning?
Logistic regression is primarily used for binary classification tasks, where the goal is to predict one of two possible outcomes, like spam vs. not spam, default vs. non-default, or pass vs. fail. It’s also extendable to multiclass classification using techniques like softmax regression.
2. What is the difference between logistic and linear regression?
The main difference lies in their purpose and output:
– Linear regression predicts continuous values, like house prices or temperatures.
– Logistic regression predicts probabilities for classification problems and maps output to a 0–1 range using the sigmoid function.
3. Why do we use the sigmoid function in logistic regression?
The sigmoid function transforms the output of a linear equation into a probability value between 0 and 1. This is crucial for classification tasks, where we want to interpret the result as the likelihood of belonging to a particular class.
4. Is logistic regression a linear model?
Yes, logistic regression is considered a linear model, not because it predicts linear output, but because the log-odds (or logit) of the probability are modeled as a linear combination of the input features.
5. When should I not use logistic regression?
Avoid using logistic regression when:
– Your data has non-linear relationships that can’t be captured through feature engineering.
– You’re working with highly imbalanced datasets and don’t plan to use techniques like class weighting or sampling.
– Your features are strongly correlated (multicollinearity), which can distort model coefficients.




























Did you enjoy this article?