
What is the Minimax Algorithm? A Beginner’s Guide
Jan 19, 2026 7 Min Read 4165 Views
(Last Updated)
Have you ever wondered how IBM’s Deep Blue chess computer famously defeated world champion Garry Kasparov in 1997? The minimax algorithm was the key decision-making strategy behind this historic victory.
The minimax algorithm in artificial intelligence is a recursive program designed to make optimal decisions in two-player games like chess and tic-tac-toe. First formalized by John von Neumann in 1928, this cornerstone of game theory helps computers minimize potential losses while maximizing opportunities to win. In contrast to simpler algorithms, minimax works by recursively building a game tree where each node represents a possible future state of the game.
This beginner-friendly guide will help you understand what the minimax algorithm is, how it works, and why it’s so important in AI decision-making. You’ll also learn about optimization techniques like alpha-beta pruning that made Deep Blue’s evaluation of millions of positions per second possible. Let’s begin!
Table of contents
- What is the Minimax Algorithm?
- Origin in game theory and AI
- Why it's important in decision-making
- How the Minimax Algorithm Works
- Game tree and players (Max vs Min)
- Evaluating terminal states
- Backpropagating utility values
- Choosing the optimal move
- Minimax Algorithm in Artificial Intelligence
- 1) Use in two-player games like chess and tic-tac-toe
- 2) Handling perfect information scenarios
- 3) Example: AI choosing the best move in tic-tac-toe
- Optimizing Minimax with Alpha-Beta Pruning
- What is alpha-beta pruning?
- How it reduces computation
- When to use it
- Strengths, Limitations, and Real-World Use Cases of the Minimax Algorithm
- 1) Advantages: optimality and clarity
- 2) Limitations: complexity and depth
- 3) Applications in robotics, economics, and games
- Concluding Thoughts…
- FAQs
- Q1. What is the main purpose of the minimax algorithm?
- Q2. How does the minimax algorithm work in chess?
- Q3. What is alpha-beta pruning and how does it improve the minimax algorithm?
- Q4. What are the limitations of the minimax algorithm?
- Q5. Where else can the minimax algorithm be applied besides games?
What is the Minimax Algorithm?
The minimax algorithm is a decision rule designed to minimize the possible loss in a worst-case scenario. Think of it as a cautious strategy that helps you make the best move by assuming your opponent will always make their optimal move.
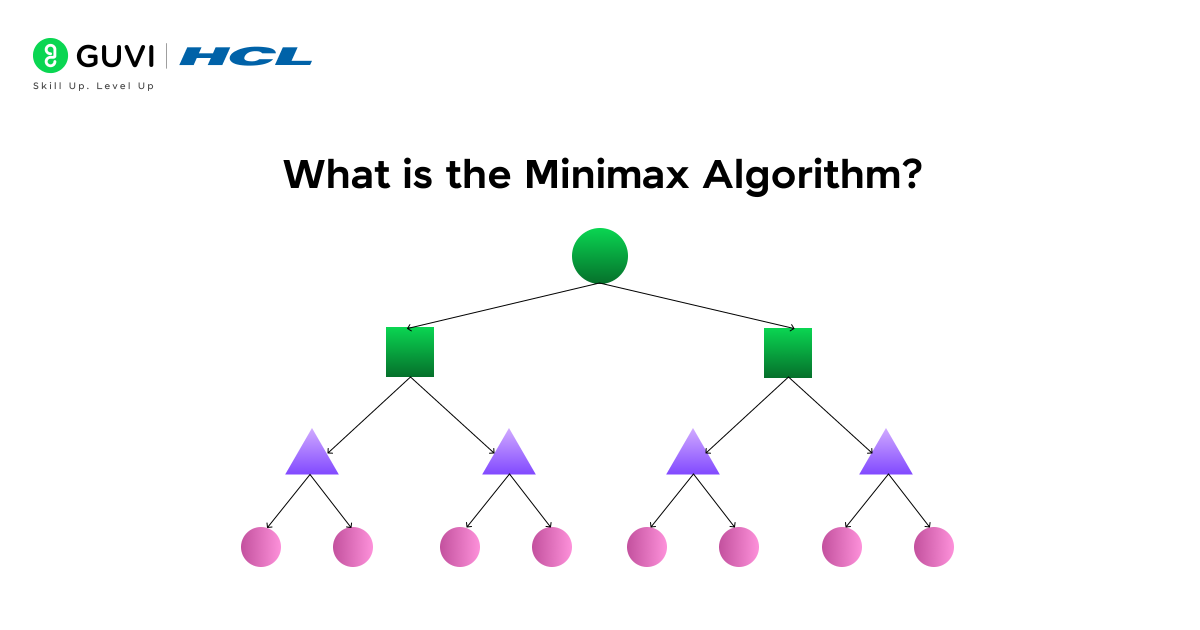
The name “minimax” perfectly captures its essence – “mini” refers to minimizing your maximum possible loss, essentially helping you make decisions that protect against worst outcomes. For games where you’re trying to maximize gains rather than minimize losses, it’s sometimes called “maximin”.
This algorithm works recursively, building a game tree where each node represents a potential game state. The two players take alternating roles:
- The maximizer (you) tries to get the highest score possible
- The minimizer (opponent) works to achieve the lowest score possible
Through this process, each position is assigned a value using an evaluation function that indicates how favorable that position is for the player.
Origin in game theory and AI
- The minimax concept has a rich history dating back to 1928 when John von Neumann first formalized it in his paper “On the Theory of Games of Strategy”. This groundbreaking work laid the foundation for modern game theory and decision-making algorithms.
- Furthermore, in 1950, Claude Shannon published a paper introducing the idea of an evaluation function and a minimax algorithm that could anticipate the effectiveness of future moves. This approach revolutionized how computers could analyze games.
- The algorithm reached mainstream recognition in 1997 when IBM’s Deep Blue chess computer, using minimax with alpha-beta pruning, defeated world champion Garry Kasparov. This historic victory demonstrated the power of minimax when combined with sufficient computing resources.
Why it’s important in decision-making
The minimax algorithm holds immense importance in decision-making for several key reasons.
First, it provides a strategic framework for making optimal decisions by considering all possible moves and their outcomes. This makes it particularly valuable in zero-sum games where one player’s gain equals the other’s loss.
Additionally, minimax excels in perfect information scenarios – games where both players have complete knowledge of all previous moves. This makes it ideal for classic games like chess, tic-tac-toe, backgammon, and Go.
Most importantly, the algorithm introduces a critical concept in artificial intelligence: the ability to look ahead and plan several moves in advance. By simulating potential future states, minimax enables computers to make decisions based not just on immediate outcomes but on long-term strategy.
The minimax approach also serves as the foundation for more sophisticated algorithms. When combined with techniques like alpha-beta pruning, it becomes even more powerful by dramatically reducing the computation needed to evaluate complex game trees.
How the Minimax Algorithm Works
The inner workings of the minimax algorithm might seem complex at first, yet its principles are surprisingly intuitive. Let’s break down this powerful decision-making process step by step.
1. Game tree and players (Max vs Min)
The minimax algorithm begins by constructing a game tree, which maps out all possible moves and their resulting states. Picture this tree as a roadmap of every possible game scenario branching out from the current position.
Within this structure, two distinct players emerge:
- The maximizer (often called MAX), who tries to achieve the highest possible score
- The minimizer (often called MIN) works to obtain the lowest possible score
Each layer of the tree alternates between MAX and MIN nodes, representing the players taking turns. This pattern mirrors how games like chess or tic-tac-toe naturally progress, with players making moves one after another.
For instance, in a typical game scenario, you (as the maximizer) would control nodes where it’s your turn to move, whereas your opponent (the minimizer) controls nodes where it’s their turn. This fundamental dynamic forms the core of how the algorithm evaluates potential outcomes.
2. Evaluating terminal states
At the bottom of the game tree lie the terminal states – positions where the game has ended with a clear outcome (win, loss, or draw). The algorithm assigns specific values to these states:
| Outcome | Typical Value |
| MAX wins | +1 or +10 |
| MIN wins | -1 or -10 |
| Draw | 0 |
These values represent the utility or desirability of each outcome from the maximizer’s perspective. In practical applications, the exact numbers may vary, yet the principle remains consistent – higher values favor MAX, lower values favor MIN.
3. Backpropagating utility values
Once terminal states are evaluated, the algorithm works backward through the tree in a process called backpropagation. This recursive approach determines the value of each intermediate node:
- At MAX nodes, select the maximum value among all child nodes
- At MIN nodes, select the minimum value among all child nodes
Mathematically, this can be expressed as:
- For MAX nodes: V(s) = max(V(s’) for all successor states s’)
- For MIN nodes: V(s) = min(V(s’) for all successor states s’)
This recursive calculation continues until reaching the root node, effectively determining the best possible outcome assuming both players make optimal moves at every turn.
4. Choosing the optimal move
Finally, after all values have been backpropagated to the root, the algorithm selects the move that leads to the child node with the most favorable value.
For the maximizer at the root position, this means choosing the action that leads to the highest-valued child node. This selection represents the move most likely to result in victory (or minimize defeat) against an opponent playing optimally.
Moreover, advanced implementations consider the depth factor when evaluating moves, preferring:
- Faster wins (subtracting depth from positive scores)
- Slower losses (adding depth to negative scores)
This refinement ensures that the algorithm not only finds winning moves but prioritizes the most efficient paths to victory, making it an exceptionally powerful tool for game-playing artificial intelligence.
Minimax Algorithm in Artificial Intelligence
The minimax algorithm represents one of artificial intelligence’s most successful strategies for decision-making in competitive scenarios. From classic board games to complex strategic challenges, this algorithm has proven its worth across numerous applications.
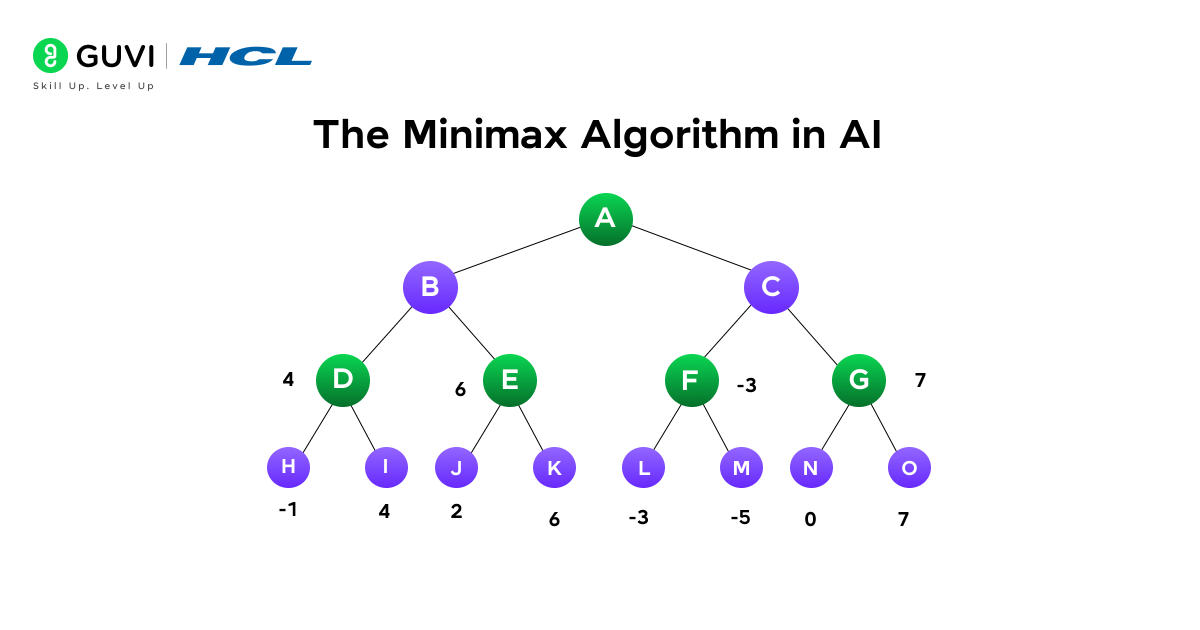
1) Use in two-player games like chess and tic-tac-toe
In the realm of artificial intelligence, the minimax algorithm shines brightest in two-player zero-sum games. These include popular games such as:
- Chess – where IBM’s Deep Blue famously used minimax with alpha-beta pruning to defeat world champion Garry Kasparov in 1997
- Tic-tac-toe – a perfect testing ground due to its manageable game tree size
- Checkers – where an AI called “Chinook” defeated champion Marion Tinsley in 1994
- Go – though more complex, still benefits from minimax principles
What makes these games ideal for minimax implementation is their deterministic nature—there’s no element of chance involved. Instead, the outcome depends entirely on player decisions, allowing the algorithm to predict and evaluate all possible future states.
The minimax strategy works by alternating between maximizing and minimizing players. In chess, for instance, every legal move from the current board state leads to a different node in the game tree. The algorithm evaluates each potential move by determining both its own and its opponent’s best strategies.
2) Handling perfect information scenarios
Minimax excels specifically in perfect information scenarios, where both players can see all aspects of the game state. This stands in contrast to games like poker, where players hold hidden cards.
In perfect information games, the algorithm operates under these key properties:
- Deterministic – The outcomes are predictable with no randomness involved
- Zero-sum – One player’s gain equals the other’s loss
- Sequential decision-making – Players take turns making moves
Through these properties, minimax ensures optimal decision-making by considering all possible moves and their outcomes within a given search depth. This strategic advantage comes from its ability to predict the opponent’s best responses and choose moves that maximize the player’s benefit.
3) Example: AI choosing the best move in tic-tac-toe
To understand how minimax works in practice, consider a tic-tac-toe scenario. Imagine an AI player (X) facing this board:
X | O | X
———
O | X |
———
| | O
The minimax algorithm would evaluate all possible moves by:
- Creating a game tree – Each node represents a potential board state after each possible move
- Evaluating terminal states – Assigning values like +1 for AI wins, -1 for human wins, and 0 for draws
- Backpropagating values – Working backward from terminal states to determine the value of each move
- Selecting optimal move – Choosing the move with the highest value
In this example, the AI would determine that placing an X in the bottom-left corner leads to a guaranteed win. Even if the human player blocks on their next turn, the AI can still force a win in a subsequent move.
The implementation follows this pattern in pseudocode:
function minimax(board, depth, is_maximizing):
if check_win(board, "X"):
return 1
if check_win(board, "O"):
return -1
if check_draw(board):
return 0
if is_maximizing:
best_score = -infinity
for each empty cell:
place "X" in cell
score = minimax(board, depth+1, false)
remove "X" from cell
best_score = max(score, best_score)
return best_score
else:
best_score = +infinity
for each empty cell:
place "O" in cell
score = minimax(board, depth+1, true)
remove "O" from cell
best_score = min(score, best_score)
return best_scoreThis recursive approach enables the AI to examine all possible futures of the game, making it impossible to defeat in simple games like tic-tac-toe when properly implemented. Nevertheless, for more complex games with larger game trees, optimizations like alpha-beta pruning become essential to make the algorithm computationally feasible.
Optimizing Minimax with Alpha-Beta Pruning
While the minimax algorithm is powerful, it faces a significant challenge: computational efficiency. This is where alpha-beta pruning comes to the rescue, dramatically improving performance without sacrificing accuracy.
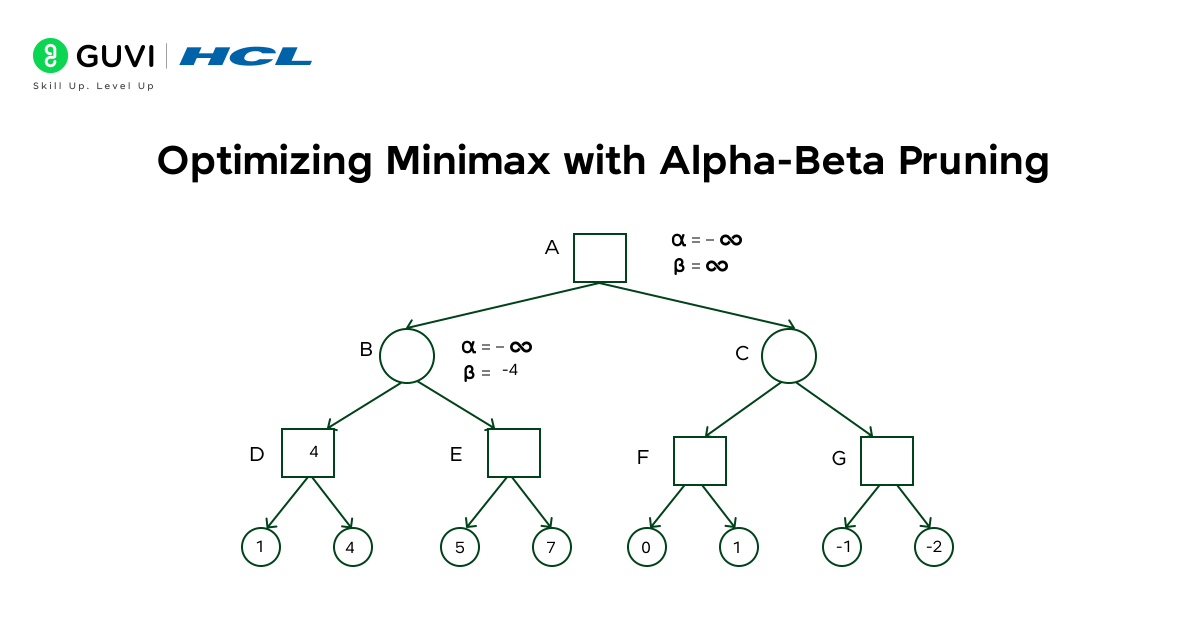
What is alpha-beta pruning?
Alpha-beta pruning is not a new algorithm but rather an optimization technique for the minimax algorithm. It works by eliminating branches in the game tree that cannot possibly influence the final decision. The technique maintains two values during tree traversal:
- Alpha (α): The best (highest) value that the maximizing player can guarantee so far
- Beta (β): The best (lowest) value that the minimizing player can guarantee so far
The algorithm stops evaluating a move when at least one possibility proves the move to be worse than a previously examined move.
How it reduces computation
The primary benefit of alpha-beta pruning lies in its ability to eliminate entire branches of the search tree. Consequently, the search can focus on more promising subtrees, allowing for a deeper search in the same amount of time.
With a branching factor of b and search depth of d plies, standard minimax evaluates O(b^d) leaf nodes. However, with optimal move ordering, alpha-beta pruning reduces this to approximately O(b^(d/2)). In practical terms, a chess program that would normally evaluate more than one million terminal nodes at four plies depth could eliminate all but about 2,000 nodes—a reduction of 99.8%.
When to use it
Alpha-beta pruning should be used whenever you implement the minimax algorithm in practical applications. It’s particularly valuable for:
- Complex games with large branching factors
- Scenarios requiring deeper search depths
- Real-time decision-making systems
Furthermore, the effectiveness of alpha-beta pruning increases with better move ordering. Examining the most promising moves first (like captures in chess) maximizes the number of branches that can be pruned.
The minimax algorithm has some fascinating historical and practical roots you might not expect:
Von Neumann’s Legacy: The algorithm was first formalized by mathematician John von Neumann in 1928, laying the foundation for modern game theory and decision-making strategies.
Claude Shannon’s Vision: In 1950, Claude Shannon—known as the “father of information theory”—suggested using minimax for computers to play chess, revolutionizing early AI research.
From theoretical mathematics to world-famous chess matches, the minimax algorithm has played a surprising role in shaping the future of artificial intelligence!
Strengths, Limitations, and Real-World Use Cases of the Minimax Algorithm
Examining the minimax algorithm beyond its mechanics reveals both its remarkable capabilities and inherent constraints in practical applications.

1) Advantages: optimality and clarity
- The minimax algorithm guarantees optimal decision-making by exhaustively analyzing all possible moves. Its deterministic nature ensures consistent, predictable outcomes without randomness.
- Furthermore, the algorithm is remarkably simple to engineer and implement, making it an accessible starting point for understanding game-playing AI.
2) Limitations: complexity and depth
- Despite its strengths, the minimax algorithm faces significant computational challenges. The algorithm’s time complexity is O(b^d), where b represents the branching factor and d is the depth.
- In chess, with an average branching factor of 35 and typical game length of 80 moves, this creates more possible states than atoms in the universe. Additionally, minimax struggles with games involving hidden information or chance elements like poker.
3) Applications in robotics, economics, and games
Beyond gaming, minimax principles extend to:
- Robotics: Helping autonomous systems navigate and allocate resources in competitive environments
- Economics: Modeling auction strategies and price negotiations between buyers and sellers
- Security systems: Predicting and countering threats in adversarial scenarios
Level up beyond algorithms like Minimax with HCL GUVI’s Intel-powered AI & ML Course, co-created with IITM Pravartak—delivering hands-on experience across Generative AI, Agentic AI, Deep Learning, and MLOps. With live weekend classes in English, Hindi, or Tamil, flexible EMI plans, and real-world projects plus placement guidance, this course bridges the gap from theory to career-ready practice
Concluding Thoughts…
The minimax algorithm stands as a fundamental concept in artificial intelligence that transforms how computers make decisions in competitive scenarios. Throughout this guide, you’ve learned how this recursive algorithm evaluates potential moves by building game trees and assigning values to different positions.
You can start implementing this powerful algorithm in simple games like tic-tac-toe to gain hands-on experience. The beauty of minimax lies in its straightforward logic – always assume your opponent will make their best move while you seek your optimal path. This foundational concept will serve you well as you explore more advanced AI decision-making strategies. Good Luck!
FAQs
Q1. What is the main purpose of the minimax algorithm?
The minimax algorithm is designed to make optimal decisions in two-player games by minimizing potential losses while maximizing opportunities to win. It works by recursively evaluating all possible moves and their outcomes, assuming that the opponent will always make their best move.
Q2. How does the minimax algorithm work in chess?
In chess, the minimax algorithm builds a game tree representing all possible moves and their resulting board states. It then evaluates these states, assigning values to each position. The algorithm works backwards from these evaluations, choosing the move that leads to the best possible outcome for the player, assuming the opponent also plays optimally.
Q3. What is alpha-beta pruning and how does it improve the minimax algorithm?
Alpha-beta pruning is an optimization technique for the minimax algorithm that significantly reduces the number of nodes evaluated in the game tree. It works by eliminating branches that cannot possibly influence the final decision, allowing for a deeper search in the same amount of time without sacrificing accuracy.
Q4. What are the limitations of the minimax algorithm?
The main limitation of the minimax algorithm is its computational complexity, especially for games with large branching factors. It can become impractical for complex games without optimizations. Additionally, the algorithm struggles with games involving hidden information or chance elements, and requires a complete game tree and predefined utility values.
Q5. Where else can the minimax algorithm be applied besides games?
Beyond gaming, the minimax algorithm and its principles have applications in various fields. It’s used in robotics for navigation and resource allocation in competitive environments, in economics for modeling auction strategies and price negotiations, and in security systems for predicting and countering threats in adversarial scenarios.





























Did you enjoy this article?