What is Perceptron in Machine Learning? A Simple Guide for Beginners (2025)

The perceptron in machine learning stands as one of the earliest supervised learning techniques. Initially, this groundbreaking algorithm received significant attention from both media and researchers as a major breakthrough toward building intelligent machines.

In fact, the perceptron serves as the cornerstone of artificial neural networks, drawing inspiration from biological neurons and enabling computers to learn, make choices, and solve complex problems. Today, understanding what a perceptron is and how it functions provides you with essential knowledge for grasping more advanced concepts in AI.

As you begin your journey into machine learning, this guide will break down the perceptron model into simple, digestible concepts. You’ll learn about different types of perceptrons, how they’re trained, and their limitations that ultimately led to more sophisticated neural network architectures. Let’s begin!

What is a Perceptron in Machine Learning?

A perceptron is a binary classifier algorithm that determines whether an input belongs to a specific category or not. Created by Frank Rosenblatt in 1957, this mathematical model processes inputs through a set of weighted connections and produces a single binary output.

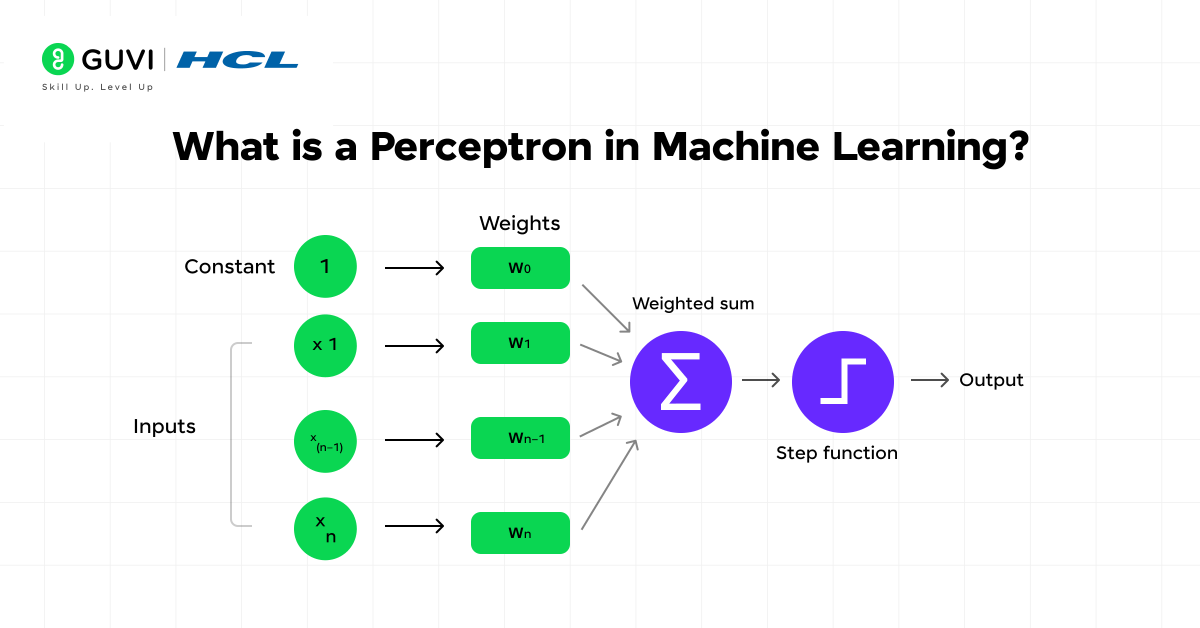
The structure of a perceptron in machine learning includes several key components:

• Inputs: Values representing features or properties of the data
• Weights: Numbers that indicate the importance of each input
• Bias: An additional parameter that helps adjust the output
• Weighted sum: The combined inputs multiplied by their respective weights
• Activation function: Typically a step function that converts the weighted sum into a binary output

The perceptron functions by taking numerical inputs, multiplying them with weights, summing these products along with the bias, and passing this sum through an activation function to generate a final classification output.

Why it matters in machine learning

The significance of perceptrons extends beyond their simple structure. As the simplest form of a neural network, perceptrons laid the groundwork for more advanced AI systems we use today.

Despite being developed over 60 years ago, the perceptron algorithm remains fundamental to how we train deep networks today. This model proved that machines could learn to recognize patterns and make predictions based on data, establishing the foundation for supervised learning techniques.

Furthermore, perceptrons demonstrated the possibility of creating computational systems that could adapt and improve over time. By adjusting weights through training, these models introduced the concept of machine learning as we understand it today.

How a Perceptron Works: Step-by-Step

Understanding how a perceptron in machine learning works requires breaking down its computational process into simple, sequential steps. The perceptron model in machine learning processes information through four key stages that transform raw inputs into meaningful classifications.

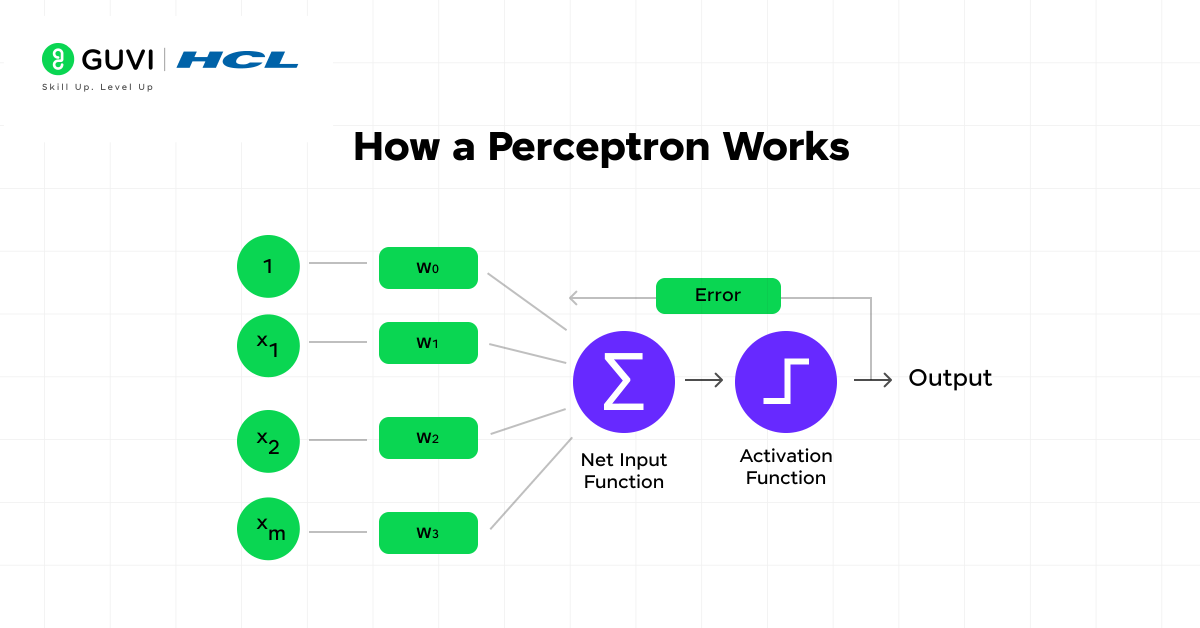
1) Inputs, weights, and bias

Every perceptron in machine learning begins with three fundamental components that drive its decision-making process:

• Inputs: These are the numerical values that represent features of the data being analyzed. In a perceptron, inputs can be binary (0 or 1) or continuous real numbers. For instance, if you’re building a perceptron to classify emails, inputs might represent features like word frequency or message length.
• Weights: Each input is assigned a specific weight that signifies its importance in the decision-making process. Higher weights indicate a stronger influence on the output. Initially, these weights might be randomly assigned, but they get adjusted during training.
• Bias: This additional parameter shifts the decision boundary away from the origin. The bias acts as another tunable parameter that improves the model’s performance even when all inputs are zero. Think of bias as the perceptron’s baseline tendency to output a particular result.

2) Calculating the weighted sum

Once you have the inputs and weights ready, the next step involves computing their weighted sum:

1. Multiply each input by its corresponding weight
2. Add all these products together
3. Add the bias term to this sum

This calculation can be expressed mathematically as: Weighted sum = (x₁ × w₁) + (x₂ × w₂) + … + (xₙ × wₙ) + b

Where x represents inputs, w represents weights, and b is the bias. This weighted sum gives an appropriate representation of the inputs based on their relative importance.

3) Applying the activation function

Subsequently, the perceptron in machine learning passes this weighted sum through an activation function that introduces non-linearity into the output. Several activation functions can be used, including:

• Heavisine step function: The most common for basic perceptrons, outputting 1 if the weighted sum exceeds the threshold and 0 otherwise
• Sign function: Similar to the step function, but outputs either +1 or -1
• Sigmoid function: Outputs values between 0 and 1, useful for probability-based outputs

The activation function essentially determines whether the perceptron in machine learning will “fire” (activate) based on the calculated value. For the Heavisine step function:

if weighted_sum >= threshold: 

    output = 1

else: 

    output = 0

4) Generating the output

The final stage produces the perceptron’s decision or prediction based on the activation function’s result. In the simplest form, the output is binary (0 or 1), representing classifications such as:

• Yes/No decisions
• True/False classifications
• Belong/Don’t belong to a category

For binary classification problems, this output represents the perceptron’s decision about which class the input belongs to. The perceptron model attempts to separate positive and negative classes by learning the optimal values for weights and bias.

During training, the weights and bias are adjusted to minimize errors, but for prediction (after training is complete), the process simply flows through these four steps to generate an output.

The beauty of the perceptron in machine learning lies in its simplicity – just four straightforward steps transform numerical inputs into meaningful classifications, forming the foundation for more complex neural networks in machine learning.

Types of Perceptron Models

Perceptron models in machine learning come in different varieties, each with distinct capabilities and applications. First of all, let’s explore the two main types of perceptron architectures that form the foundation of neural network development.

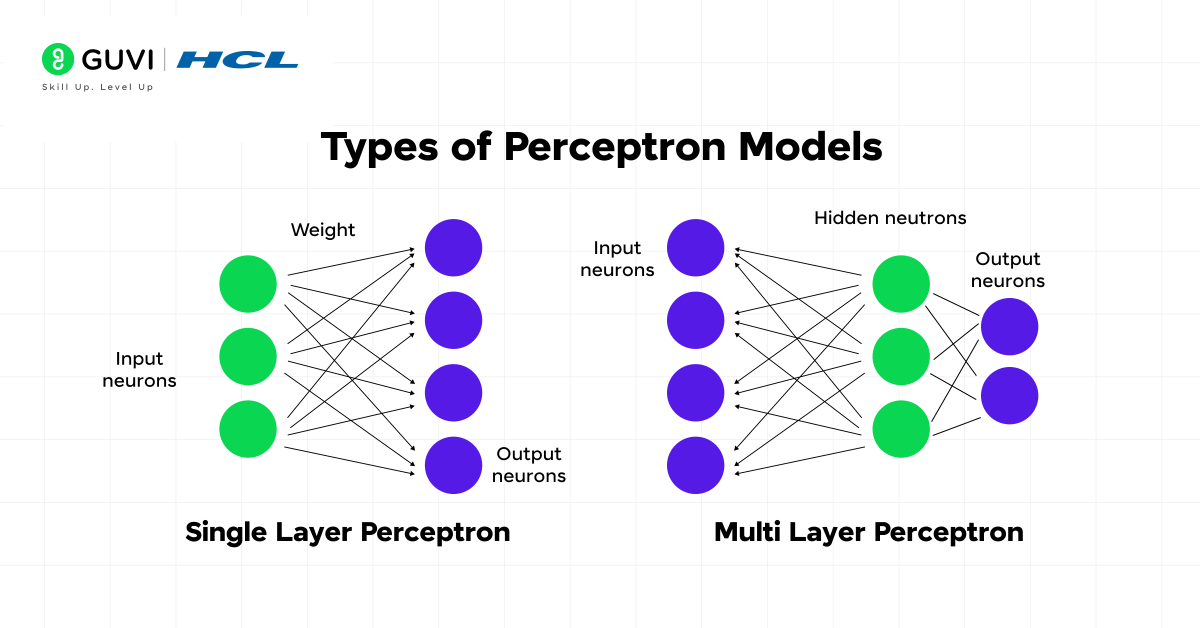
1) Single-layer perceptron: basics and use cases

The single-layer perceptron in machine learning (SLP) represents the original and most basic form of neural network, first introduced by Frank Rosenblatt in 1958. This foundational model consists of just an input layer directly connected to an output layer with no hidden layers between them.

How an SLP works:

• Takes inputs from the input layer
• Applies weights to these inputs and sums them
• Passes this sum through an activation function to produce output

A single-layer perceptron in machine learning is particularly effective for tasks involving linearly separable data – situations where a straight line can cleanly divide input data into distinct categories. Primarily, SLPs excel at computing logical operations like AND, OR, and NOR gates that have binary inputs and outputs.

The original perceptron in machine learning used a step function that only produced 0 or 1 as output, though modern implementations often use sigmoid activation functions because they’re smoother and work better with gradient-based learning methods.

2) Multi-layer perceptron: structure and power

In contrast, a multi-layer perceptron (MLP) contains one or more hidden layers positioned between the input and output layers. This more advanced architecture forms the basis of deep learning and can handle data that isn’t linearly separable.

The structure of an MLP includes:

• An input layer that receives data
• One or more hidden layers with neurons using nonlinear activation functions
• An output layer that produces predictions

MLPs evolved specifically to overcome the limitations of single-layer perceptrons. Notably, they function as universal approximators, meaning they can model virtually any continuous function with sufficient neurons in their hidden layers. This capability makes them extraordinarily versatile for complex pattern recognition tasks.

Each layer in an MLP connects fully to the next layer, creating a dense network of interconnections that enables the processing of intricate relationships within data. Additionally, MLPs use continuous activation functions such as sigmoid or ReLU, rather than step functions, which enables more nuanced outputs and efficient learning.

Training a Perceptron: Learning Algorithm Explained

The perceptron learning algorithm enables machine learning models to improve through experience. This supervised learning method teaches perceptrons how to classify data by adjusting their weights based on errors.

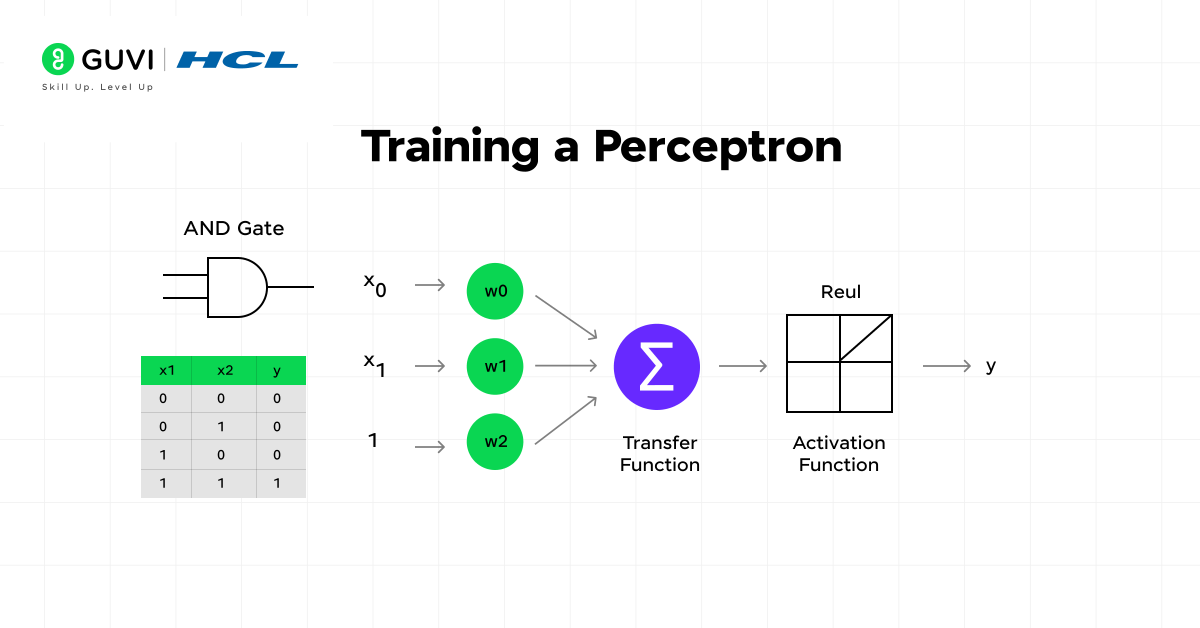
A) What is the perceptron learning rule?

The perceptron learning rule is a supervised training algorithm that adjusts weights and bias to minimize classification errors. It forms the foundation of neural networks by allowing perceptrons to learn from labeled examples.

Primarily, this rule works by:

• Comparing the perceptron’s output with the correct target value
• Calculating the error between the prediction and the actual value
• Adjusting weights and bias accordingly to reduce errors

This learning process follows a forward propagation step (making predictions) followed by backward propagation (adjusting weights based on errors).

B) Perceptron learning algorithm example

Let’s examine the AND gate problem as a simple example. For this binary classification task:

1. Start with random weights (e.g., w₁ = 0.9, w₂ = 0.9) and set a learning rate (0.5)
2. For input (0,0):
   • Weighted sum = (0×0.9) + (0×0.9) = 0
   • Activation output = 0 (correct, no weight update needed)
3. For input (0,1):
   • Weighted sum = (0×0.9) + (1×0.9) = 0.9
   • Activation output = 1 (incorrect, should be 0)
   • Update weights: w₁ = 0.9 – 0.5 = 0.4, w₂ = 0.9 – 0.5 = 0.4

The algorithm continues through all training examples, adjusting weights whenever a misclassification occurs.

C) How weights and bias are updated

The mathematical formula for updating weights is:

w_new = w_old + η(y – ŷ)x

Where:

• w_old is the current weight
• η (eta) is the learning rate
• y is the actual target value
• ŷ is the predicted output
• x is the input value

Similarly, the bias is updated using:

b_new = b_old + η(y – ŷ)

The error term (y – ŷ) determines both the direction and magnitude of weight adjustments. When the prediction matches the target (y = ŷ), no update occurs.

D) Convergence and stopping criteria

The perceptron learning algorithm will converge if the data is linearly separable, meaning a hyperplane exists that can perfectly separate the classes. Accordingly, the algorithm continues until:

• All training examples are correctly classified, or
• A maximum number of iterations (epochs) is reached

The Perceptron Convergence Theorem guarantees that for linearly separable data, the algorithm will find a solution after a finite number of iterations.

The learning rate significantly influences convergence speed. A large learning rate helps the model learn faster but might reduce accuracy, whereas a smaller learning rate improves accuracy but requires more training time. Typical practice involves testing learning rates on a logarithmic scale between very small values (like 0.0001) and 1.0.

Limitations and the Path to Deep Learning

Despite their innovations, early perceptrons faced serious limitations that temporarily halted progress in neural network research during the 1960s and 70s.

1) The linear separability problem

Single-layer perceptrons can only solve linearly separable problems—those where you can draw a straight line to separate different classes of data. This fundamental constraint means that many real-world problems remain unsolvable with basic perceptron models. 

Much like trying to separate oil and water with a straight stick, some patterns simply cannot be classified with linear boundaries.

2) The XOR problem and its impact

The XOR (exclusive OR) problem became the classic example demonstrating perceptron limitations. It follows this truth table:

• Input (0,0) → Output 0
• Input (0,1) → Output 1
• Input (1,0) → Output 1
• Input (1,1) → Output 0

Since this pattern requires a non-linear decision boundary, single-layer perceptrons fail to solve it. Minsky and Papert highlighted this limitation in their influential 1969 book “Perceptrons,” which led to reduced funding and triggered an “AI winter”.

3) How multi-layer perceptrons solved it

Multi-layer perceptrons (MLPs) finally overcame these limitations by introducing hidden layers between input and output. These hidden layers effectively transform the input space, making non-linearly separable problems like XOR become linearly separable.

Through this transformation, MLPs can create complex decision boundaries and approximate virtually any continuous function. This breakthrough ultimately paved the way toward modern deep learning architectures and rekindled interest in neural networks.

Master AI end-to-end—from Python basics, statistics and machine learning fundamentals to advanced Deep Learning, Generative AI, LLMs and Agentic AI—while gaining hands-on experience with tools like PyTorch, TensorFlow, Docker, MLOps, and cloud platforms. This 6-month, IIT-M Pravartak & Intel-certified AI/ML Course includes live weekend classes, real-world capstone projects, and mentorship to build your technical portfolio and launch your AI-ML career.

Concluding Thoughts…

The perceptron in machine learning stands as a fundamental milestone in machine learning history. Through this guide, you’ve learned how this simple computational model mimics biological neurons to make binary classifications based on weighted inputs. Despite being developed over 60 years ago, perceptrons remain remarkably relevant to understanding today’s complex AI systems.

Understanding perceptrons gives you a solid foundation before diving into more advanced neural network architectures. The concepts of inputs, weights, activation functions, and learning algorithms remain consistent throughout neural network theory, though they grow increasingly complex.

I hope this guide helps you begin your learning journey into perceptrons and do reach out to me in the comments section below if you have any doubts. Good Luck!

FAQs

Q1. What is a perceptron in machine learning? 

A perceptron is a simple algorithm in machine learning that mimics how biological neurons process information. It’s designed for binary classification tasks, such as determining whether an email is spam or not, by using weighted inputs to make decisions.

Q2. How does a perceptron work? 

A perceptron works by taking numerical inputs, multiplying them with assigned weights, summing these products along with a bias, and then passing this sum through an activation function to generate a binary output (typically 0 or 1).

Q3. What are the limitations of a single-layer perceptron? 

Single-layer perceptrons can only solve linearly separable problems, meaning they can only classify data that can be separated by a straight line. They cannot handle complex, non-linear problems like the XOR problem.

Q4. How do multi-layer perceptrons differ from single-layer perceptrons? 

Multi-layer perceptrons (MLPs) have one or more hidden layers between the input and output layers, allowing them to solve non-linear problems. They can approximate virtually any continuous function, making them more versatile for complex pattern recognition tasks.

Q5. What is the perceptron learning rule? 

The perceptron learning rule is a supervised training algorithm that adjusts the weights and bias of a perceptron to minimize classification errors. It compares the perceptron’s output with the correct target value, calculates the error, and adjusts the parameters accordingly to improve performance over time.