
Recursion Algorithms in DSA? Understanding Logic, Types, and Applications
Nov 26, 2025 7 Min Read 2196 Views
(Last Updated)
Have you ever wondered how a function can solve a problem by calling itself? Recursion is one of the most powerful ideas in computer science because it lets complex tasks be broken down into smaller and more manageable steps. From sorting large datasets to traversing trees and solving logical puzzles, recursion simplifies many operations that seem complicated at first glance.
To understand how recursion algorithms work, its components, and where it fits best in programming, read the complete blog for clear insights and real examples.
Table of contents
- What is a Recursion Algorithms?
- Components of a Recursive Algorithm
- Base Case
- Recursive Case
- Recurrence Relation
- Mathematical Representation of a Recursive Problem
- Explanation
- Example Walkthrough
- Types of Recursion Algorithm
- Direct Recursion
- Indirect Recursion
- Tail Recursion
- Non-Tail Recursion
- Linear Recursion
- Tree Recursion
- Mutual Recursion
- Examples of Recursive Algorithms
- Step-by-Step Execution Flow of a Recursive Algorithm
- Applications of the Recursion Algorithm
- Sorting and Searching Algorithms
- Tree and Graph Traversal
- Mathematical and Combinatorial Computations
- Backtracking and Constraint Solving
- Dynamic Programming and Memoization
- Recursion vs Iteration
- Limitations of the Recursion Algorithm
- Conclusion
- FAQs
- Can recursion affect program performance?
- What skills help in mastering recursion in DSA?
- Can recursion be used for non-mathematical problems?
- When should I use recursion instead of iteration?
What is a Recursion Algorithms?
A recursion algorithm is a technique where a problem is solved by breaking it into smaller versions of itself until reaching a simple case that can be handled directly. Each step calls the same function with a modified input, which creates a chain of executions that eventually resolves backward toward the final answer.
For example, calculating a factorial uses recursion because each call multiplies the current number by the factorial of the smaller one. Recursion simplifies complex logic into compact code and strengthens the connection between mathematical reasoning and programming practice.
Components of a Recursive Algorithm
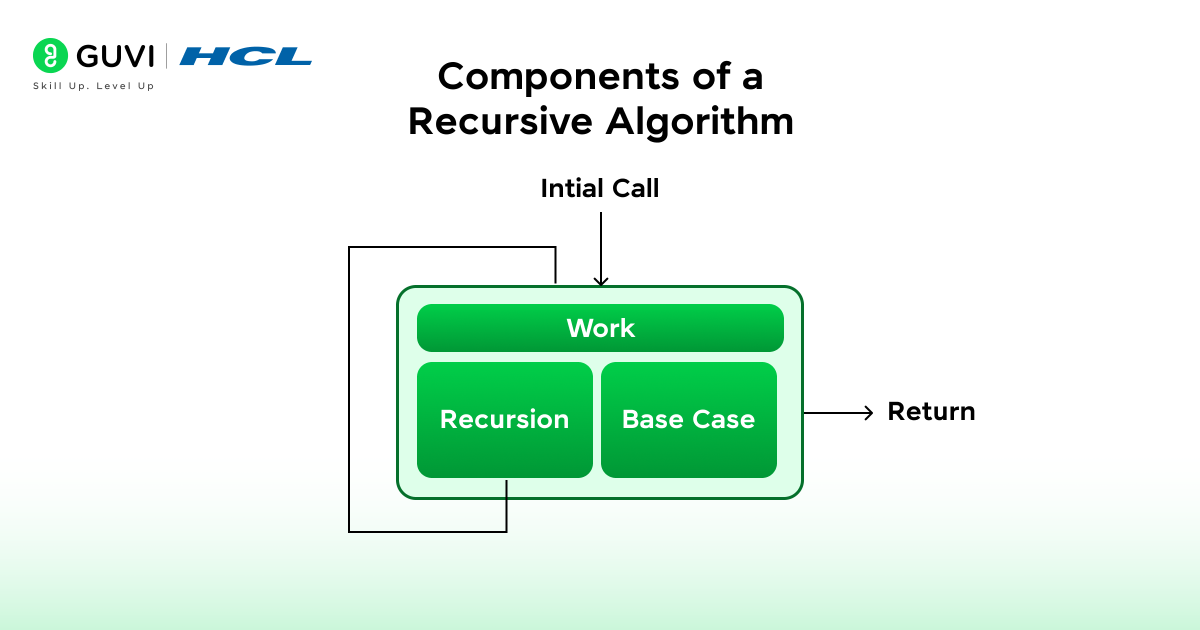
1. Base Case
The base case serves as the stopping point of recursion. It defines the smallest version of the problem that can be solved directly without further calls. Without a base case, recursion would continue indefinitely, consuming stack memory and never reaching completion. The base case ensures stability and correctness within the algorithm.
In computing factorial values, the base case is defined as factorial(1) = 1. The function halts there because the value no longer depends on any smaller computation. This stopping rule allows all previous recursive calls to return results step by step until the final answer forms.
2. Recursive Case
The recursive case represents the active process of reducing the problem into smaller parts. Each recursive call processes a simpler subproblem that moves closer to the base condition. This step gives recursion its repetitive yet structured behavior and defines how the function self-references to reach a solution.
In the factorial calculation, each recursive call multiplies the current number by the factorial of one less number. The repeated reduction process continues until the function meets the base condition, ensuring that each subsequent computation is supported by the previous one.
3. Recurrence Relation
A recurrence relation acts as the mathematical description of how each recursive step connects to the previous one. It defines the dependency between subproblems and sets the rate at which the recursion converges toward the base case. This relation is often written as an equation to represent the growth or reduction pattern in recursive algorithms.
For example, the relation for factorial can be expressed as T(n) = T(n−1) + O(1), which means each recursive call performs one constant-time operation and one smaller subproblem call. This formal definition helps analyze the time complexity and efficiency of recursive methods in DSA.
Mathematical Representation of a Recursive Problem
A recursive algorithm can be formally expressed using a recurrence relation that defines how a problem is divided into smaller parts. Each recursive structure contains two key elements: the base case and the recursive step, which together describe how the function progresses and terminates.
The general form can be written as:
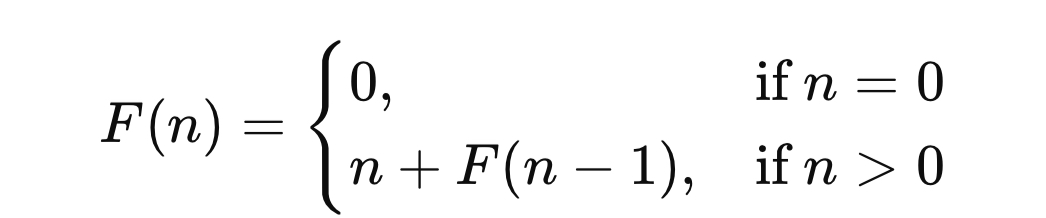
Explanation
- Base Case: The base case handles the simplest version of the problem, where no further breakdown is needed. Here, when n=0n=0, the recursion stops and returns 0.
- Recursive Step: The recursive step reduces the problem into a smaller instance. Each call computes F(n)=n+F(n−1)F(n)=n+F(n−1), gradually simplifying until the base case is reached.
Example Walkthrough

This pattern clearly illustrates how recursion builds a complete solution from smaller and repeated computations.
Types of Recursion Algorithm

1. Direct Recursion
A direct recursion occurs when a function in a data structure algorithm calls itself inside its own body. It progressively reduces the problem size with each call until the base condition halts further execution.
Key Features:
- Function directly calls itself without involving another function.
- Simple to trace and debug because the call chain follows one path.
- Commonly used for problems that naturally divide into smaller versions of themselves.
Example:
def factorial(n):
if n == 0:
return 1
return n * factorial(n – 1)
This function multiplies n by the factorial of (n-1) until it reaches 0, producing n!.
2. Indirect Recursion
Indirect recursion happens when one function calls another, and that second function calls the first one again.
Key Features:
- Involves two or more functions calling each other in sequence.
- Useful when logic separation improves readability or modularity.
- Requires careful base conditions to prevent infinite calls.
Example:
def funcA(n):
if n > 0:
print(n)
funcB(n – 1)
def funcB(n):
if n > 0:
print(n)
funcA(n – 1)
Here, funcA and funcB call each other until n becomes zero.
3. Tail Recursion
Tail recursion performs the recursive call as the last action in the function. The compiler can optimize it to reuse the current function frame.
Key Features:
- Reduces memory usage because stack frames are reused.
- Eliminates the need to wait for results after returning from recursion.
- Often used where results can be accumulated during calls.
Example:
def tail_factorial(n, result=1):
if n == 0:
return result
return tail_factorial(n – 1, n * result)
Each recursive call passes the current result, avoiding deferred multiplications.
4. Non-Tail Recursion
In non-tail recursion, the recursive call is followed by another operation, so each function waits for its child call to finish.
Key Features:
- Memory usage increases as all calls stay in the stack until completion.
- Common problems require post-processing after recursion.
- Easier to apply in hierarchical data structures.
Example:
def print_descending(n):
if n > 0:
print(n)
print_descending(n – 1)
The print statement happens before the recursive call, keeping the structure active until all calls resolve.
5. Linear Recursion
Linear recursion triggers one recursive call at each step, forming a single chain of calls.
Key Features:
- Simple control flow with predictable stack usage.
- Each call handles one smaller version of the problem.
- Works well for straightforward numerical or sequential problems.
Example:
def sum_n(n):
if n == 0:
return 0
return n + sum_n(n – 1)
Each call adds one number to the total until n becomes zero.
6. Tree Recursion
Tree recursion occurs when a function makes multiple recursive calls within one execution.
Key Features:
- Expands the recursion tree exponentially.
- Used when subproblems overlap, as in divide-and-conquer algorithms.
- Can be optimized using memoization or dynamic programming.
Example:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n – 1) + fibonacci(n – 2)
Each call splits into two more calls until the smallest cases return values.
7. Mutual Recursion
Mutual recursion involves two or more functions calling one another in a repeated cycle.
Key Features:
- A structured variant of indirect recursion with alternating function calls.
- Useful in logic-based systems and alternating task flows.
- Needs clearly defined base conditions to avoid infinite loops.
Example:
def is_even(n):
if n == 0:
return True
return is_odd(n – 1)
def is_odd(n):
if n == 0:
return False
return is_even(n – 1)
Each function delegates part of the problem to the other until the base case ends the cycle.
Examples of Recursive Algorithms
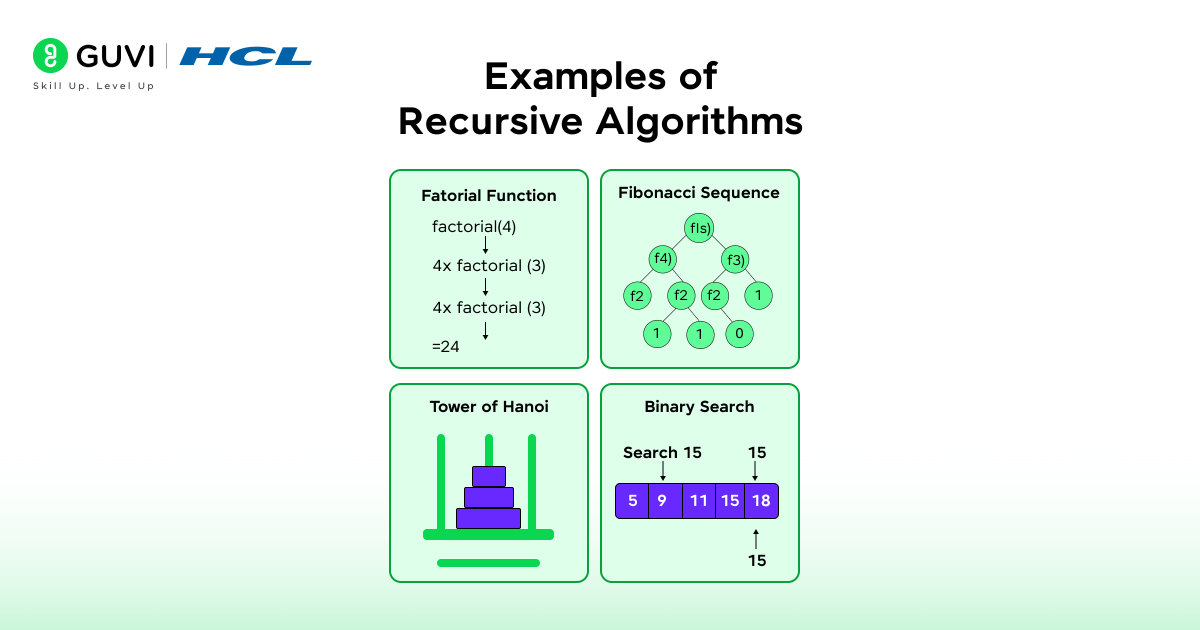
- Factorial Function
The factorial algorithm multiplies a number by the factorial of its preceding number until it reaches one. It demonstrates how recursion expresses mathematical repetition through direct function calls. The process starts with the given number and works backward until it arrives at the base value.
Example: To compute factorial(4), the program performs 4 × factorial(3), then 3 × factorial(2), then 2 × factorial(1). Once it reaches factorial(1)= 1, the recursion ends, and the results combine to produce 24.
- Fibonacci Sequence
The Fibonacci sequence builds each term as the sum of the previous two. The recursive approach expresses this naturally because each function call calculates two smaller values and adds them together. Although elegant, this algorithm grows exponentially unless optimized with memoization.
Example: To calculate fibonacci(5), the program calls fibonacci(4) and fibonacci(3). Each of these further expands until reaching the base values of Fibonacci (0) = 0 and Fibonacci (1) = 1. The final output combines these results to form the value 5.
- Tower of Hanoi
The Tower of Hanoi problem reflects recursion through physical movement logic. It involves transferring disks between rods under strict rules. The recursive design handles smaller sets of disks before addressing the main move, ensuring each step maintains proper order.
Example: With three disks, recursion moves the top two disks to an auxiliary rod. It shifts the largest disk to the target rod and then moves the two smaller disks onto it. Each recursive call focuses on one smaller movement pattern until all disks align correctly.
- Binary Search
Binary search applies recursion to locate an element in a sorted array. Each step compares the target value with the middle element and continues the search in the relevant half. This division continues until the element is found or the search range becomes empty.
Example: To find 15 in [5, 9, 11, 15, 18], the algorithm checks the middle element 11. Since 15 is greater, it searches the right half and finds 15 at the next recursive step. The process completes in logarithmic time due to consistent halving of the data range.
Bring your AI ideas to life: build powerful, production-ready software with our AI Software Development Course. Learn how to integrate models, design APIs, deploy scalable AI systems, and maintain code quality, all from industry experts. Get hands-on experience, build real projects, and transform your skills from theory to product-ready capabilities. Enroll today and start building the AI solutions of tomorrow!
Step-by-Step Execution Flow of a Recursive Algorithm
- Initialization of the Function Call: The process begins with the initial input passed to the recursive function. This input sets the context for the first evaluation and establishes the range of recursion that will follow.
- Base Case Evaluation: The algorithm checks whether the input satisfies the base condition. If it does, recursion halts immediately and returns a result that forms the foundation for all previous calls to resolve.
- Recursive Case Execution: If the base condition is not met, the function proceeds to call itself with modified inputs. Each recursive call simplifies the problem and moves it one step closer to the base case.
- Stack Frame Expansion: Every recursive call creates a new stack frame in memory. These frames hold intermediate data and return points. The stack grows downward with each call until the base case is reached.
- Unwinding and Result Composition: After reaching the base case, the recursive calls begin to resolve in reverse order. Each function retrieves the result from its deeper call, performs its operation, and returns it upward. This reversal completes the computation chain that connects all recursive levels.
Applications of the Recursion Algorithm

1. Sorting and Searching Algorithms
Recursive techniques form the base of quicksort, merge sort, and binary search. These algorithms repeatedly divide data until reaching atomic units, ensuring efficient processing in O(log n) or O(n log n) time.
2. Tree and Graph Traversal
Depth-first traversals in trees and graphs rely on recursion to visit nodes in sequence without explicit stack usage. This simplifies exploration and maintains order naturally.
3. Mathematical and Combinatorial Computations
Recursion simplifies computing factorials, Fibonacci numbers, GCD, and combinations. It breaks mathematical definitions into actionable steps aligned with their recursive expressions.
4. Backtracking and Constraint Solving
Used in complex problems like the N-Queens puzzle, Sudoku solver, and maze navigation. Recursion facilitates exploring all possibilities and reverting (backtracking) when a constraint fails.
5. Dynamic Programming and Memoization
Recursive approaches combined with memoization help solve overlapping subproblems efficiently (e.g., computing Fibonacci numbers, shortest paths, or knapsack optimization).
Recursion vs Iteration
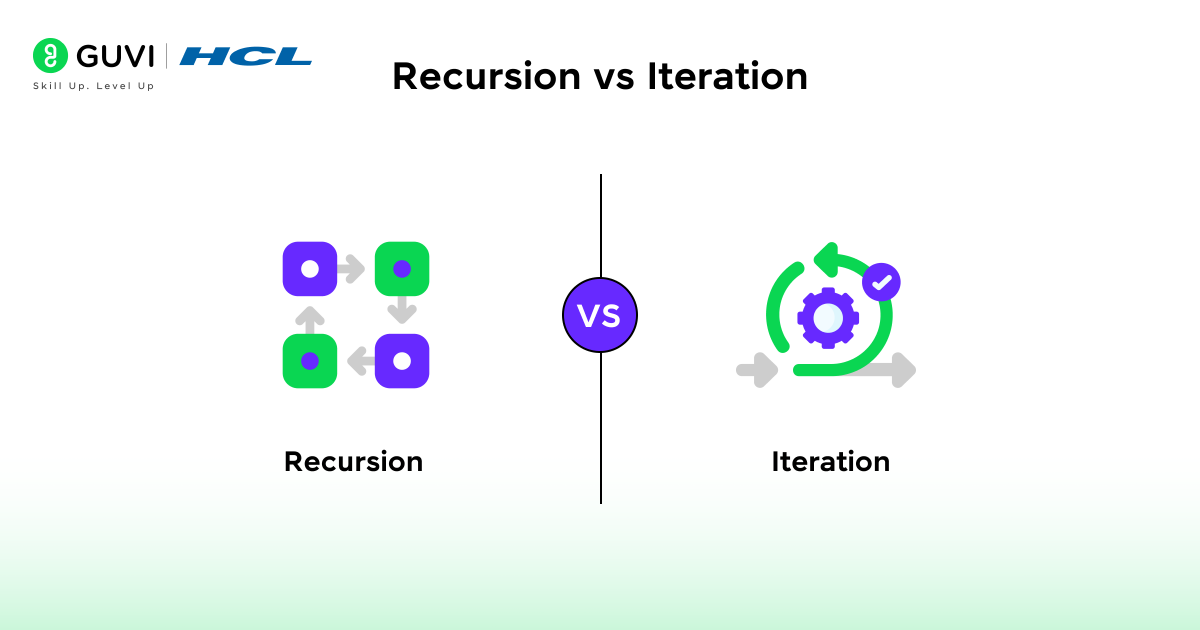
| Factor | Recursion | Iteration |
| Definition | A method where a function calls itself to solve smaller subproblems. | A method that repeatedly executes a set of instructions using loops until a condition is met. |
| Termination | Stops when it reaches the base case. | Stops when the loop condition becomes false. |
| Memory Usage | Consumes more memory due to multiple call stack frames. | Uses less memory since variables are updated in place. |
| Speed | May be slower due to function call overhead. | Usually faster because it avoids repeated function calls. |
| Code Structure | Compact and closer to mathematical definitions. | Requires explicit control structures such as for or while loops. |
| Debugging | More difficult because of multiple recursive calls. | Easier to trace since the flow is linear. |
| Best Suited For | Problems with hierarchical or self-referential structures like trees and graphs. | Problems that involve simple repetitions or fixed number of iterations. |
| Example | Computing factorial using factorial(n) = n * factorial(n – 1). | Computing factorial using a loop that multiplies numbers from 1 to n. |
Limitations of the Recursion Algorithm
- High Memory Usage: Recursive algorithms require additional memory because each call adds a new frame to the call stack. Large input sizes or deep recursion can exhaust available memory and cause stack overflow errors. This becomes more critical in problems that lack clear base conditions or require extensive branching.
- Slower Execution in Some Cases: Recursion can increase execution time because of repeated function calls and stack operations. Each call involves overhead related to parameter passing and return handling. Problems that can be solved with direct iteration may perform faster without recursion.
- Difficulty in Debugging and Tracing: Tracing the flow of recursive calls is often complex. Errors in base or recursive conditions may cause infinite loops or incorrect outputs. Understanding how data passes through multiple recursive layers requires careful step-by-step analysis.
- Limited Suitability for Simple Problems: Recursion may overcomplicate problems that can be solved with straightforward iteration. The added cost of function calls and stack maintenance may not justify the benefits of recursion for smaller tasks. Choosing the correct approach requires balancing readability and performance.
- Risk of Stack Overflow: Each recursive function call consumes space on the call stack. Deep or infinite recursion can fill the stack, which leads to runtime failure. This limitation makes recursion less practical for tasks that involve unpredictable or extremely large inputs.
Want to master how recursion powers algorithms from factorials to tree traversals? Learn to design, trace, and optimize recursive logic step by step with our Data Structures & Algorithms using Java Course. Gain hands-on experience with recursion, dynamic programming, and divide-and-conquer strategies used in top coding interviews and real-world applications. Strengthen your DSA foundation and elevate your problem-solving confidence today!
Conclusion
Recursion stands as one of the most essential concepts in DSA because it connects mathematical reasoning with algorithmic execution. It reflects how large problems can be expressed through smaller and similar subproblems. Each recursive call contributes to solving one layer of the problem until the complete result emerges. This structure promotes logical flow and precision in problem-solving. A clear grasp of recursion prepares programmers to tackle complex data problems efficiently and with precision.
FAQs
1. Can recursion affect program performance?
Yes. Recursive algorithms can use more memory and processing time if not carefully designed. Deep recursion may lead to a stack overflow, which can be avoided by using tail recursion or converting the logic into an iterative form.
2. What skills help in mastering recursion in DSA?
Understanding base and recursive cases, analyzing recurrence relations, and practicing trace execution are key. Regularly solving problems involving trees, graphs, and mathematical patterns strengthens recursive reasoning.
3. Can recursion be used for non-mathematical problems?
Yes. Recursion is not limited to mathematical computations. It is frequently used in non-mathematical problems such as navigating file systems and traversing trees. It helps in solving puzzles like Sudoku or N-Queens, and managing hierarchical data in applications.
4. When should I use recursion instead of iteration?
Recursion is best used when a problem can be divided into smaller and similar subproblems that depend on previous results. It is ideal for tree traversal and divide-and-conquer algorithms problems. Iteration is better suited for repetitive tasks with a predictable number of steps.

























Did you enjoy this article?