Applications of Linked Lists in Data Structure

Have you ever wondered why linked lists remain relevant in DSA even when arrays, vectors, and high-level containers already exist? The reason is simple: most real systems do not deal with neatly fixed data, and linked lists offer a level of structural freedom that static storage can never match. They reshape themselves as data grows, shrink without wasting memory, and connect elements through logic rather than position. That is why they appear in compilers, operating systems, runtime allocators, graph engines, editors, schedulers, and everywhere data refuses to stay still.

If you want a deeper breakdown of how linked lists power real software, explore the full blog to learn more.

What is a Linked List in Data Structure? 

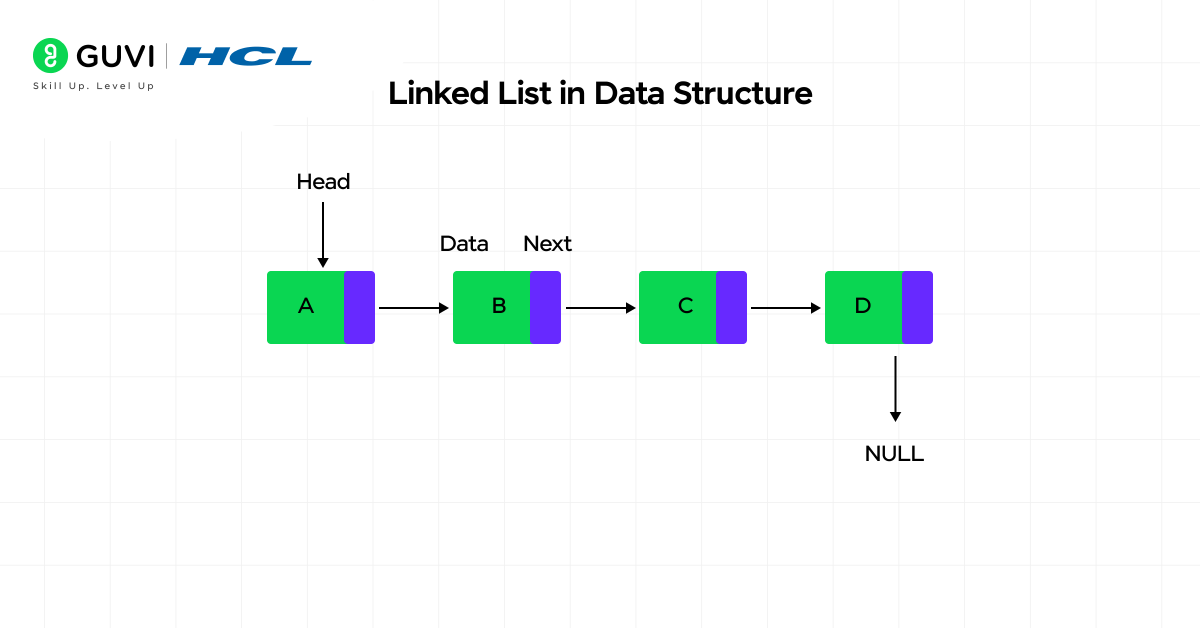
A linked list in DSA is a linear data structure where elements, called nodes, are connected through pointers rather than stored in a continuous memory block. Each node contains data and a reference to the next node, which makes insertion and deletion faster than in arrays because elements do not need to be shifted in memory. The structure supports flexible memory use because nodes are created only when required instead of reserving a fixed block in advance.

Types of Linked List in Data Structure

1. Singly Linked List

A singly linked list forms a one-way chain of nodes where every node stores a single pointer to its successor. This linear flow keeps the structure lightweight, which makes it suitable for applications where memory footprint matters more than bidirectional access.

Key Highlights:

• Requires minimal pointer storage per node
• List growth is unrestricted because nodes are allocated on demand
• Commonly used in stack-like structures and simple traversal tasks

2. Doubly Linked List

A doubly linked list extends the idea of a single link by adding a pointer to the previous node. This dual linkage supports quick movement in either direction, which benefits algorithms that frequently backtrack or modify nodes in the middle.

Key Highlights:

• Supports constant-time deletion even without tracking the previous node manually
• Allows symmetric traversal, which improves search paths in certain data sequences
• Preferred in applications such as browser history tracking and LRU caches

3. Circular Linked List

A circular linked list removes the concept of a terminal node by linking the last node back to the first. This looping nature provides equal access to every node without resetting traversal, which gives it an advantage in repetitive processing cycles and makes it an important concept to understand when you learn DSA.

Key Highlights:

• Eliminates null pointer checks during traversal
• Ideal for systems that run in cycles such as time-sharing schedulers
• Useful in implementing buffer rotations and continuous data streams

4. Circular Doubly Linked List

A circular doubly linked list combines two-way navigation with looping continuity. Every node connects to both its neighbors, and the structure has no absolute start or end, which grants full flexibility in direction and sequence control.

Key Highlights:

• Supports insertion or removal at any position with uniform cost
• Suitable for programs that require seamless forward and backward cycling such as media playlists
• Often used in advanced simulations and real-time state tracking where no index is fixed

Also, Read: How to Improve Your DSA Skills? Complete Guide

Top 10 Applications of Linked Lists in Data Structures and Algorithms (DSA) 

1. Implementing Other Data Structures

Linked lists serve as a flexible foundation for several abstract data types because they allow elements to be inserted, removed, and rearranged without relying on fixed-size memory. Their ability to grow and shrink through pointer manipulation gives them a structural advantage in scenarios where storage demand changes at runtime. This adaptability supports multiple higher-level data models, leading to the following implementations:

• Stacks: Operates through constant-time pointer switching at the top node and supports use cases such as recursive call tracking, arithmetic expression parsing, and session backtracking.
• Queues: Maintains uninterrupted data flow in systems such as task pipelines, device buffers, and print spooling services because enqueue and dequeue depend only on pointer updates.
• Deques: Allows modification at both the front and rear in equal time, which benefits sliding window tasks, palindrome validation, and priority alternation structures.

2. Collision Handling in Hash Tables

Hash tables require a mechanism to store multiple keys that map to the same index, and linked lists offer a flexible way to manage those collisions without forcing a full table resize or secondary probing strategy. By attaching extra elements through node linking rather than fixed indexing, the structure remains operational even when the load factor increases. 

This leads to several practical collision-resolution methods:

• Separate Chaining: Stores colliding keys at the same index through a linked structure, isolating collision costs within a single bucket rather than across the full table.
• Sorted Bucket Linking: Maintains ordered nodes inside a bucket, which reduces search steps for lookups that fall within the same slot.
• Expandable Collision Groups: Buckets grow by appending new nodes instead of reallocating arrays, which postpones expensive rehash operations during scale-up.

3. Graph Representation

Graphs often contain a large number of vertices but a limited number of actual connections, making full matrix storage wasteful. Linked lists enable a graph to store only existing edges, which aligns memory usage with real connectivity instead of theoretical maximum space, and this principle becomes especially valuable when learning DSA for system design where scalability and resource efficiency matter.

This representation supports both directed and undirected models, leading to several direct advantages:

• Adjacency List Storage: Each vertex links only to its connected nodes, which scales efficiently for sparse graphs and supports fast neighbor traversal.
• Localized Edge Modification: Adding or removing an edge adjusts only one list, avoiding restructuring of a global matrix.
• Weighted Edge Embedding: Each link node can include attributes such as distance, capacity, or cost, enabling algorithmic use without separate metadata storage.

4. Dynamic Memory Management

Memory allocators use linked lists to track free and allocated segments because they allow blocks to be reused, merged, or reassigned without relocating entire regions of memory. This model prevents wasted space and enables adaptive memory distribution during program execution. 

The use of linked tracking supports several allocator behaviors:

• Free Block Indexing: Unused segments remain linked, which allows the allocator to locate a candidate block without scanning a full linear range of memory.
• Coalescing Adjacent Blocks: Neighboring free nodes can be merged into a larger unit, reducing long-term fragmentation.
• Strategy-Driven Allocation: First-fit, best-fit, and next-fit algorithms operate directly on the linked list structure instead of pre-sorted tables.

5. Garbage Collection

Automatic memory cleanup relies on the ability to trace which objects remain in use, and linked structures allow collectors to walk through reachable data instead of scanning entire heaps blindly. This targeted traversal reduces processing time and supports multi-phase collection models. Several key processes benefit from linked organization:

• Reachability Traversal: Live objects are followed pointer by pointer, separating active memory from reclaimable space.
• Reclaim List Formation: Released nodes are linked into a reusable chain, which shortens allocation time for future objects.
• Generational Segmentation: Objects are grouped by lifetime in linked layers, allowing short-lived data to be collected more often than stable data.

Also, Read: DSA Syllabus : Learn Algorithms and Data Structures Efficiently

6. Polynomial Representation

Polynomials involve terms with distinct exponents, and storing them in linked nodes prevents wasted memory and simplifies expression manipulation. Each term becomes a self-contained node, allowing insertions and deletions without shifting an entire array of powers. This produces multiple computational benefits:

• Ordered Term Linking: Terms remain arranged by exponent, allowing linear-time arithmetic during addition or subtraction.
• Sparse Storage Support: Only coefficients that actually exist occupy memory, which is useful in symbolic math and high-degree equations.
• Direct Term Modification: Operations such as differentiation, integration, or term merging affect only individual nodes rather than full data blocks.

7. Undo and Redo Systems

Many interactive applications must preserve a sequence of user actions so that past states can be revisited or reinstated. Linked lists allow each action to remain connected to its predecessor and successor without storing redundant full snapshots. 

This design supports reversible workflows through the following behaviors:

• Bidirectional State Linking: Each change references the previous and next state, supporting controlled reverse and forward movement.
• Memory-Aware History Pruning: Old states can be detached when limits are reached, without disturbing the active action chain.
• Session-Level Persistence: Entire state histories can be serialized and restored while preserving structural order.

8. File System Management

File systems frequently store data in scattered disk regions, and linked allocation allows files to remain readable even when blocks are not stored consecutively. Instead of forcing contiguous space, each block records the location of the next block, maintaining logical order despite physical fragmentation. This creates several advantages:

• Linked Block Sequences: File content can be read sequentially even if it occupies multiple non-adjacent storage areas.
• Directory Entry Linking: File and folder records can be inserted or removed by updating pointers rather than rebuilding directory tables.
• Traceable Recovery Paths: Broken or orphaned chains can be reconstructed by following stored block links during repair operations.

9. Playlist and Route Control

Applications that manage sequences of items, such as songs, video queues, or navigation routes require structures that allow items to be modified while in use. Linked lists support flexible sequencing where order can shift without reallocation or mass copying. 

This leads to several functional benefits:

• Editable Playback Order: Items can be added, skipped, or rearranged through link updates rather than full list reconstruction.
• Route Reconfiguration: New checkpoints or detours can be inserted directly into the linked path structure.
• Looped or Cyclic Flow: Circular lists allow automatic repetition without index resetting logic.

10. Sparse Matrix Handling

Storing sparse matrices in a full two-dimensional array wastes space because most positions hold zero. Linked storage keeps only active values and their coordinates, allowing matrix operations to work on meaningful data only. This creates computational and memory efficiency in large scientific and mathematical workloads:

• Row-Linked Element Chains: Each row contains a chain of non-zero values, reducing storage cost significantly in high-dimension data.
• Column-Oriented Traversal Option: A parallel linked representation enables algorithms that operate vertically across the matrix.
• Selective Computation: Arithmetic operations touch only stored nodes, saving both time and memory bandwidth during matrix multiplication and transformation.

Transform your programming foundation into high-impact AI applications by enrolling in our AI Software Development Course. Master full-stack software skills while integrating AI models, deploying real-world systems, and staying ahead in a future powered by intelligent automation.

Best Practices for Working with Linked Lists

1. Choose the Right Variant: Select singly, doubly, or circular linked lists based on traversal needs rather than using a single type everywhere.
2. Track Head and Tail Pointers Carefully: Maintain clear references for both ends of the list to avoid unnecessary traversal during insertions or deletions.
3. Use Sentinel Nodes When Helpful: Dummy head or tail nodes can simplify edge-case handling and reduce conditional checks in code.
4. Avoid Excessive Traversal: Store extra pointers or indexes when frequent middle access is required instead of walking the list repeatedly.
5. Free Memory Explicitly in Manual-Allocation Languages: Always release node memory in languages like C or C++ to prevent leaks and dangling pointers.
6. Validate Pointers Before Access: Null checks and boundary checks prevent crashes caused by invalid memory access during traversal.
7. Prefer Iterative Traversals Over Deep Recursion: Long recursive calls risk stack overflow, while iterative loops handle large lists safely.
8. Minimize Pointer Updates in Critical Sections: In multithreaded systems, pointer changes should remain atomic to avoid race conditions and corrupted links.
9. Use Structuring Functions, Not Inline Logic: Encapsulate operations like insert, delete, and search into reusable methods to keep code readable and maintainable.
10. Document Node Relationships Clearly: Always indicate whether links are one-way, two-way, or circular to prevent logical errors during modification.

Strengthen your grasp of core data structures with our DSA using Java Course. Master linked lists, stacks, queues, and trees through real-world coding practice. Build the algorithmic foundation every top developer relies on to write efficient, scalable programs.

Conclusion 

Linked lists continue to play an essential role in DSA because they solve problems that fixed-size and contiguous structures cannot handle. Their proficiency to grow, shrink, reorder, and link elements without shifting data makes them valuable in systems where memory is fragmented, data changes frequently, and structure must adapt in real time. They support everything from abstract data types to file systems and mathematical models. Their relevance is not based on age but on capability, which is why they remain a core concept in computer science education and real software engineering, especially for learners trying to understand the difference between data structures and algorithms in real problem-solving. Mastering linked lists builds a stronger foundation for advanced data structures and scalable program design.

FAQs

1. Why are linked lists important in DSA compared to arrays?

Linked lists are preferred when frequent insertion and deletion operations are required because nodes can be modified without shifting elements in memory. Arrays may offer faster indexing, but linked lists provide better flexibility when data size changes at runtime.

2. What are the main operations performed on a linked list?

The primary operations include insertion, deletion, traversal, searching, and updating node data. Each operation works through pointer adjustments rather than index-based access, which makes performance depend on node traversal instead of direct indexing.

3. How does memory allocation work in a linked list?

Each node in a linked list is stored separately in memory and linked through pointers. This means memory is allocated dynamically for every new node instead of reserving a fixed block in advance, which helps reduce unused space in variable-sized datasets.