Graphs are an important part of Data Structures and Algorithms (DSA) because they help represent relationships between different objects. You can think of graphs as a network of connected points — for example, cities connected by roads, people connected on social media, or webpages linked to each other.

To work with graphs in programming, we need a clear way to store and manage these connections. One of the most popular and simple methods is the adjacency matrix. It helps us represent all the relationships between graph nodes in a neat, structured form that computers can easily process.

In this blog, you’ll learn everything about the adjacency matrix — what it means, how it works, how to create one in your program, and when to use it. We’ll also compare it with other graph representations, discuss its benefits and drawbacks, show code examples, and look at real-life uses. By the end, you’ll have a clear understanding of how the adjacency matrix helps in solving graph-related problems in DSA.

What Is an Adjacency Matrix?

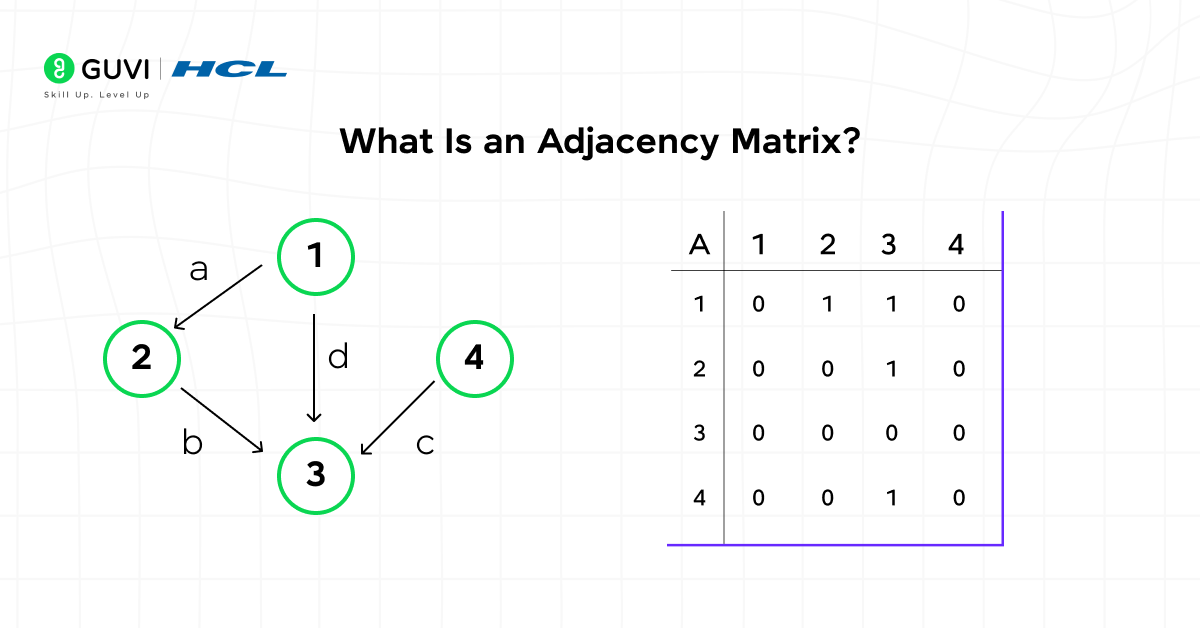
An adjacency matrix is a simple and structured way to represent a graph in programming. It is a two-dimensional array (N × N), where N is the total number of vertices (or nodes) in the graph. Each row and column of this matrix represents a vertex, and the value stored at any cell shows whether there is a connection (edge) between two vertices.

In simple words, an adjacency matrix tells us which nodes are connected to which, and how they are connected. This makes it one of the easiest ways to store and visualize relationships in a graph.

Here’s how it works:

• For unweighted graphs, the adjacency matrix contains 1 if there is an edge between two vertices and 0 if there is no edge.
  
• For weighted graphs, instead of using 1 and 0, we store the weight or cost of the edge. If no edge exists, we usually mark it as 0, -1, or INF (infinity).
  
• In directed graphs, the direction of the edge matters. So, if there is an edge from A to B, the value at matrix[A][B] will be 1, but matrix[B][A] might still be 0.
  
• In undirected graphs, the connections are two-way. That means the adjacency matrix is symmetric — if matrix[A][B] = 1, then matrix[B][A] = 1 too.

The main advantage of using an adjacency matrix is that it allows you to quickly check if an edge exists between two nodes in constant time O(1). This makes it highly efficient for operations where fast edge lookup is required, such as in graph traversal or shortest-path algorithms.

In short, an adjacency matrix in DSA is like a table that keeps track of all possible connections in a graph — making it easier to perform computations, analyze structures, and build algorithms efficiently.

Why Use an Adjacency Matrix?

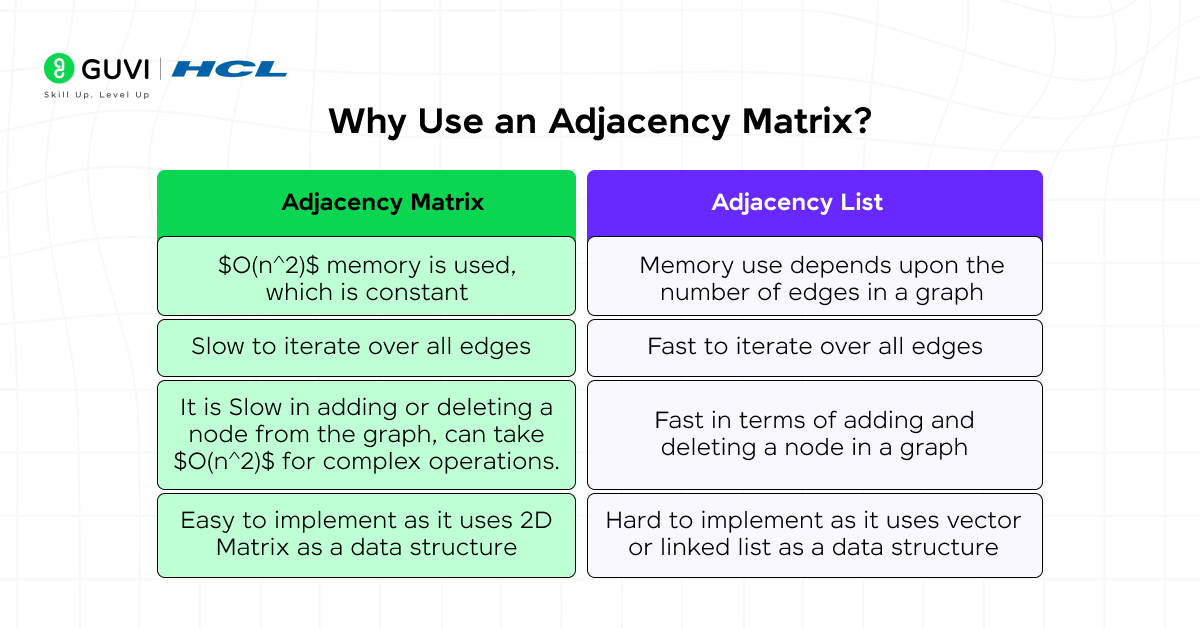
An adjacency matrix is one of the most efficient ways to represent a graph when you need quick access to connections between nodes. It provides a clear, table-like structure that allows fast and direct checking of whether an edge exists between any two vertices.

You should use an adjacency matrix in the following situations:

• When you need fast edge checks:
  If you often need to verify whether two nodes are connected, an adjacency matrix is perfect. You can find this information instantly in O(1) time because each cell directly stores the connection status.
  
• When the graph is dense:
  A graph is called dense when it has many edges — close to the total possible number of edges (N²). In such cases, using an adjacency matrix makes sense because most cells in the matrix will contain valid connections, making the memory usage worthwhile.
  
• When your algorithm relies on quick lookups:
  Some algorithms, like the Floyd–Warshall algorithm (used to find shortest paths between all pairs of vertices), perform operations on every pair of nodes. The adjacency matrix works best here because it allows immediate access to every connection without searching through lists.

However, there’s one major drawback: an adjacency matrix always takes up O(N²) space. This means that even if your graph has very few connections (a sparse graph), the matrix still occupies memory for every possible pair of vertices. So while it’s excellent for dense graphs and quick lookups, it’s not memory-efficient for large or sparse graphs.

To truly understand why and when to use an adjacency matrix, learning the core data structures and algorithms behind it is essential. HCL GUVI’s DSA eBook helps you master these basics — from arrays and matrices to graphs and dynamic programming — with clear explanations, real examples, and practice questions. It’s an ideal companion for beginners and interview aspirants who want to build strong graph fundamentals.

How to Create and Maintain an Adjacency Matrix 

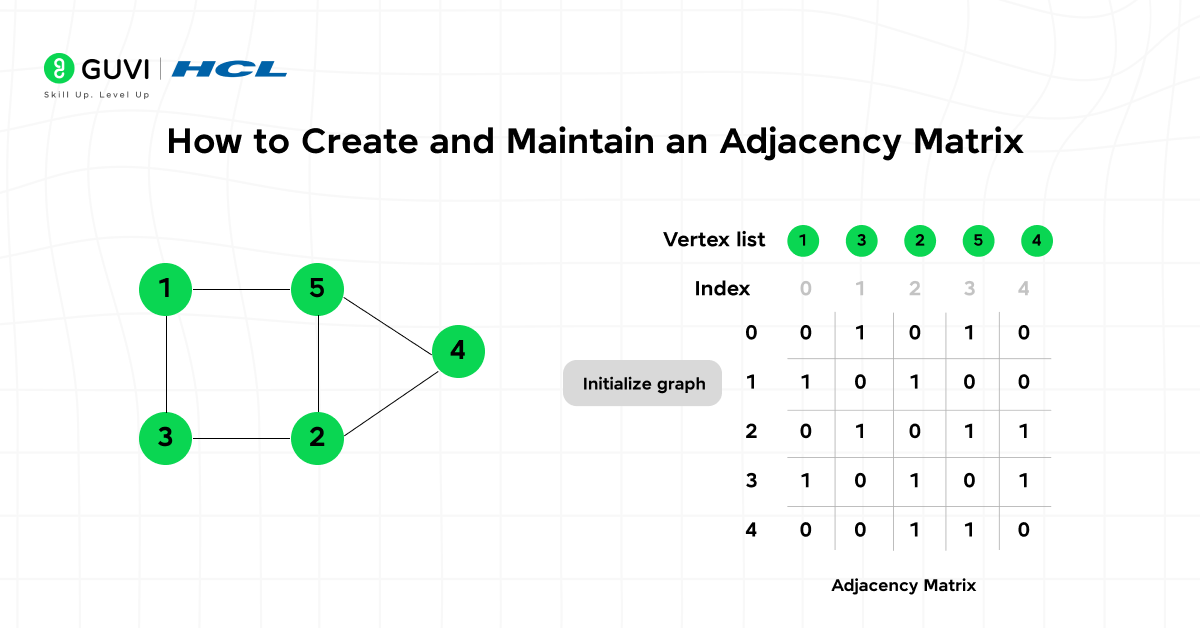
An adjacency matrix is one of the most popular and easy-to-understand ways to represent a graph in programming. Whether you are working with a simple unweighted graph or a complex weighted and directed one, understanding how to create, update, and maintain an adjacency matrix is an essential DSA skill.

Let’s break down the entire process step by step using simple terms, clear explanations, and practical code examples.

1. Initialization

The first step in creating an adjacency matrix is initializing the structure.

If a graph has N vertices, you’ll need an N × N matrix (a two-dimensional array) where each cell represents a possible connection between two nodes.

• For unweighted graphs:
  You can initialize every cell with 0, meaning “no edge exists.”
  When you add an edge between two nodes, you’ll change the corresponding entries to 1.
  
• For weighted graphs:
  You usually initialize every cell with a large number like INF (infinity) or sometimes -1 to indicate “no connection.”
  If the graph allows self-loops, set the diagonal entries (where a node connects to itself) to 0 since the distance from a node to itself is zero.

This setup makes it easy to modify and check connections later.

2. Adding an Edge

Once your matrix is initialized, you can add an edge between two vertices.

• For an undirected graph:
  Since the connection goes both ways, you must update both [u][v] and [v][u] entries to 1 (or to the edge weight in case of weighted graphs).
• For a directed graph:
  The edge goes in one direction, so you only update [u][v] and leave [v][u] unchanged.

Adding an edge takes O(1) time — meaning it’s instant, regardless of how large your graph is.

3. Removing an Edge

To remove an edge, simply reset the corresponding entries in the matrix:

• In an unweighted graph, set the value back to 0.
• In a weighted graph, set it to INF or -1 again to show that no edge exists.

This operation also takes O(1) time.

4. Checking if an Edge Exists

The biggest advantage of an adjacency matrix is how fast you can check whether an edge exists between two nodes.

You just look at the cell [u][v]:

• If it’s 1 (or any valid weight), an edge exists.
• If it’s 0 (or INF), no connection exists.

This check happens in constant time O(1) — one of the key reasons adjacency matrices are used in graph algorithms that require frequent lookups.

5. Iterating Through Neighbors

To find all the neighbors (connected vertices) of a particular node, you can scan its entire row in the matrix.

For example, to find all nodes connected to vertex u, check every column in row u and collect the indices where a connection exists (matrix[u][v] == 1).

This takes O(N) time per vertex because you have to check every possible node once.

6. Python Example 

Before jumping into the code, let’s understand what unweighted and weighted graphs mean.

• Unweighted Graph: In an unweighted graph, every edge is treated equally. It only shows whether a connection exists or not — there’s no concept of distance or cost. For example, if cities are connected by roads but we don’t care about how long the roads are, it’s an unweighted graph.
  
• Weighted Graph: In a weighted graph, every edge has a specific value (weight) that represents cost, distance, or strength of connection. For example, if roads between cities have distances in kilometers, the distance becomes the weight of the edge.

1. Python code for unweighted graph

# Adjacency matrix for unweighted undirected graph
N = 5
adj = [[0] * N for _ in range(N)]

def add_edge(u, v):
    adj[u][v] = 1
    adj[v][u] = 1  # undirected graph

def remove_edge(u, v):
    adj[u][v] = 0
    adj[v][u] = 0

def has_edge(u, v):
    return adj[u][v] == 1

# Example usage
add_edge(0, 1)
add_edge(1, 2)
print(has_edge(0, 1))  # True
print(adj)

This code demonstrates how to add, remove, and check edges in a simple graph structure.

2. Python code for weighted graph

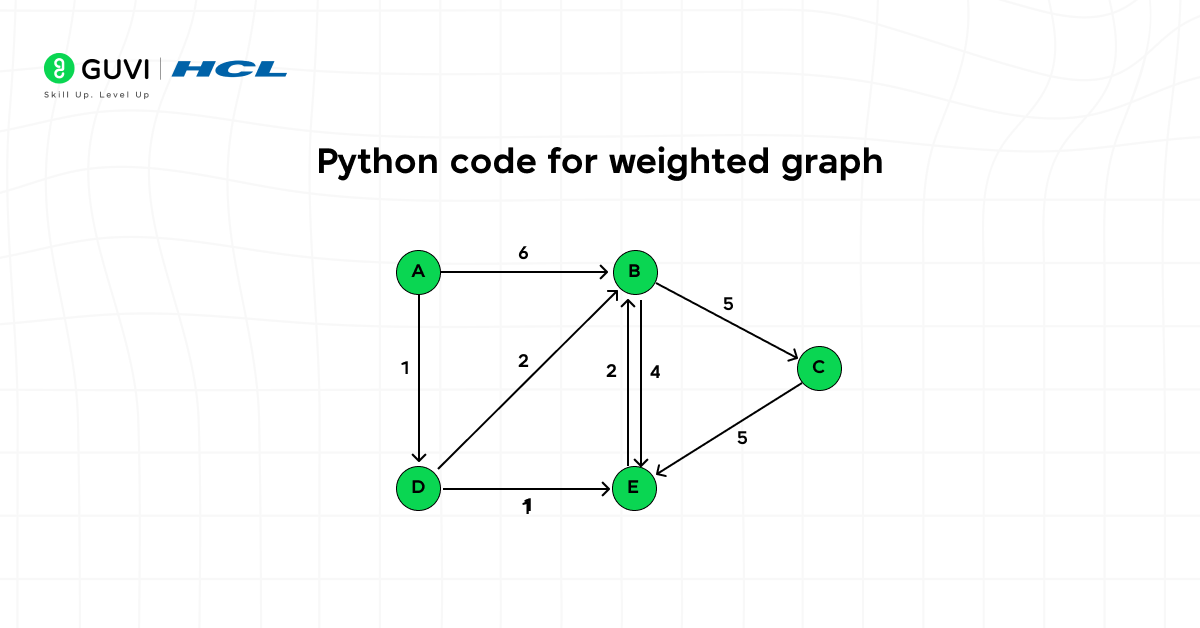
If your graph has weights and directions, you can use the following version:

INF = 10**9  # a large number representing 'no edge'
N = 4
adj = [[INF] * N for _ in range(N)]

for i in range(N):
    adj[i][i] = 0  # distance from a node to itself

def add_edge(u, v, w):
    adj[u][v] = w  # directed edge from u to v with weight w

# Example edges
add_edge(0, 1, 5)
add_edge(1, 2, 3)

# Example: adj[0][1] == 5, adj[1][0] == INF

This version is ideal for algorithms like Dijkstra or Floyd–Warshall that use edge weights.

Algorithms That Commonly Use Adjacency Matrix

• Floyd-Warshall (All Pairs Shortest Path) — natural with matrix inputs.
• Some implementations of Prim’s algorithm for dense graphs use an adjacency matrix.
• Graph algorithms that rely on repeated constant time edge checks.
• Matrix power methods for counting paths of length k (using repeated matrix multiplication).

Time and Space Complexity 

Let’s understand how efficient an adjacency matrix really is:

• Space Complexity: O(N²)
  Each vertex pair requires a cell, so memory usage grows with the square of the number of vertices.
• Check if edge exists: O(1)
  You can check for a connection instantly.
• Add or remove an edge: O(1)
  Just update one or two entries.
• Iterate through all neighbors of a node: O(N)
  You must scan the entire row.
• Iterate through all edges: O(N²)
  You’ll need to check every cell of the matrix.

This means adjacency matrices are best suited for dense graphs, where the number of edges (E) is close to N². For sparse graphs (where there are far fewer edges), adjacency lists are usually more memory-efficient.

Common Pitfalls and How To Avoid Them

• Using Matrix for Very Large Graphs: Avoid adjacency matrix when NNN is large (e.g., N>104N > 10^4N>104) unless the graph is dense — memory will explode.
• Assuming Symmetry Without Checking: For directed graphs, don’t assume matrix[u][v] == matrix[v][u].
• Memory Allocation Overhead: In languages like Python, a list of lists has overhead per list; consider using arrays/NumPy or bitsets for compact storage when performance matters.

Advantages and Disadvantages 

Advantages

• Constant time edge lookup O(1)O(1)O(1).
• Simple to implement.
• Easy to convert to matrices used in algorithms (e.g., for matrix multiplication interpretations of graph problems).
• Works naturally with linear algebra and matrix-based graph algorithms.

Disadvantages

• Space inefficient for large NNN and sparse graphs.
• Scanning neighbors requires O(N)O(N)O(N) time even if a node has few neighbors.
• Not suitable for very large graphs (e.g., millions of nodes).

Real-World Examples and Use Cases

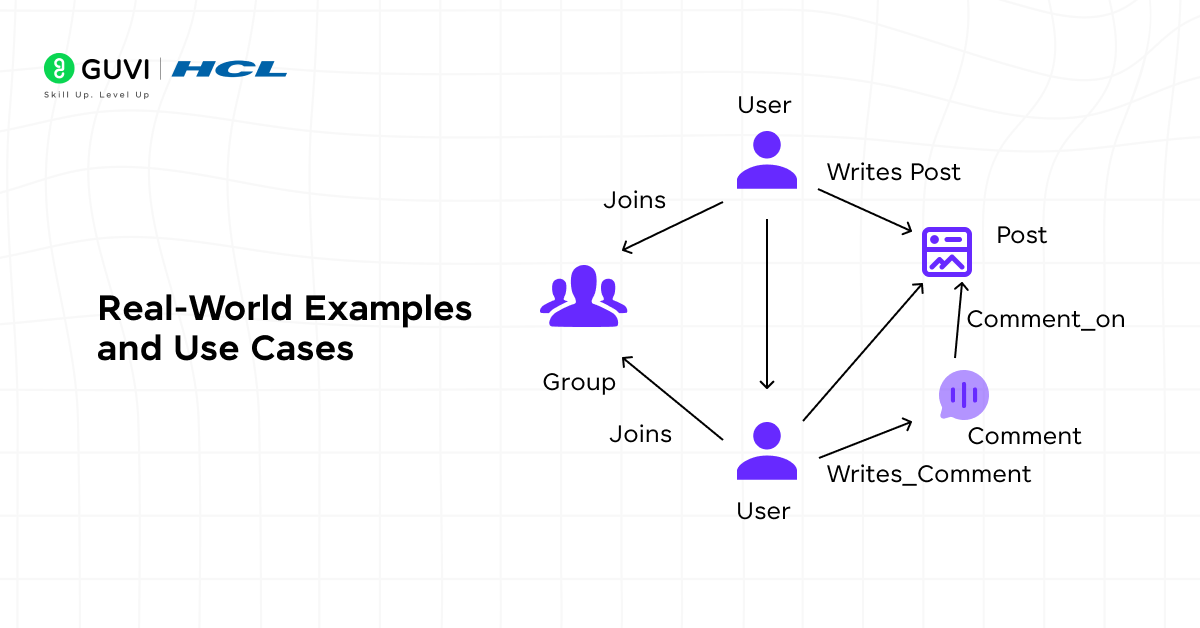
The adjacency matrix is not just an abstract DSA topic — it’s something that appears in many real-life systems we use every day. Here are some simple, relatable examples that show where and how adjacency matrices can be applied:

1. Social Media Friendships
Imagine you have a small group of friends on a social media app. Each person can follow or be friends with others.
If you make a table where both rows and columns represent people, and you mark a 1 wherever two people are connected, that table is an adjacency matrix.
For example:

• If Alice and Bob are friends, you’ll have a 1 at Alice → Bob and Bob → Alice.
• If Alice is not connected to John, that cell stays 0.
  This makes it easy for the app to instantly check who is connected to whom.

2. City Map or Road Network
Think about a few cities connected by roads — for instance, Chennai, Bengaluru, and Hyderabad.
Each city can be a vertex, and each road can be an edge.

• If a direct road connects Chennai to Bengaluru, mark it as 1.
• If there’s no direct road between Chennai and Hyderabad, mark it as 0.
  If you include distances (like 350 km between two cities), you can use weights in the matrix instead of just 1 and 0. This helps navigation apps quickly find the shortest routes between places.

3. Airline Flight Routes
Airlines use adjacency matrices to manage direct flight routes between airports.

• If there’s a direct flight from Delhi to Mumbai, mark that as 1.
• If there’s no direct flight between two cities, it stays 0.
  When you add flight durations or costs as weights, it becomes easy to calculate the shortest or cheapest route.

4. Classroom Connections or Team Projects
Imagine you have five students working together on different projects. Some students collaborate often, while others don’t.
You can make an adjacency matrix where:

• Each student is a row and column.
• A 1 means they’ve worked together.
• A 0 means they haven’t.
  This helps visualize group dynamics or teamwork patterns — similar to how project managers track collaborations.

5. Internet or Computer Networks
When multiple computers are connected in a small office network, each device is a node, and each cable or Wi-Fi link is an edge.
The adjacency matrix can show which computers can directly communicate. This is useful for network troubleshooting or data transfer optimization.

In short, the adjacency matrix helps us model and manage relationships — whether between people, cities, airports, students, or computers. It’s a simple yet powerful way to represent real-world connections clearly and efficiently.

Conclusion

The adjacency matrix is one of the simplest and most powerful ways to represent graphs in DSA. It provides instant edge lookups and a clear structure that’s easy to understand and implement. Because of its O(N²) memory requirement, it works best for dense graphs, where most nodes are connected to each other. However, for very large or sparse graphs, it’s often better to use an adjacency list to save space.

Understanding how an adjacency matrix works — along with its strengths and limitations — helps you choose the right graph representation for your algorithm. Whether you’re working on pathfinding, network design, or graph traversal, mastering this concept lays a strong foundation for advanced topics like BFS, DFS, Dijkstra’s, and Floyd–Warshall algorithms.

If you want to gain practical experience in building and optimizing graph algorithms, consider joining the HCL GUVI’s DSA using python course as it offers mentor-led sessions, hands-on coding practice, and real-world projects that help you strengthen your DSA skills and become job-ready.

FAQs

1. What exactly is the adjacency matrix in DSA used for?

It stores connections between every pair of vertices in an N×NN \times NN×N grid. It is used to quickly test the presence of an edge between two nodes and to run matrix-friendly graph algorithms.

2. When should I prefer an adjacency list over an adjacency matrix?

Prefer adjacency lists when the graph is sparse (E≪N2E \ll N^2E≪N2), because lists use O(N+E)O(N + E)O(N+E) space, are more memory efficient, and neighbor iteration is proportional to degree.

3. How do weighted edges appear in the adjacency matrix?

Instead of 1 and 0, a weighted adjacency matrix stores the weight value in matrix[u][v], and a sentinel (like INF) when no edge exists.

4. Can adjacency matrices handle directed graphs?

Yes. For directed graphs the matrix is not necessarily symmetric; matrix[u][v] may differ from matrix[v][u].

5. Are there memory-efficient variants of adjacency matrix for large graphs?

Yes — bitsets, compressed sparse row (CSR), coordinate (COO) formats, and storing only upper/lower triangles for undirected graphs are common optimizations.