Bucket Sort in DSA: A Comprehensive Tutorial

Sorting is one of the most fundamental problems you’ll learn in computer science, and most people are introduced to it through algorithms like Bubble Sort, Insertion Sort, or Merge Sort.

But there’s another algorithm that often gets overlooked, even though it can outperform many common sorting techniques under the right conditions: Bucket Sort.

It’s a simple idea with powerful implications, especially when your data is distributed in a predictable way. Let’s break it down in a way that actually makes sense, even if you’re just getting started with algorithms in this article!

What Is Bucket Sort?

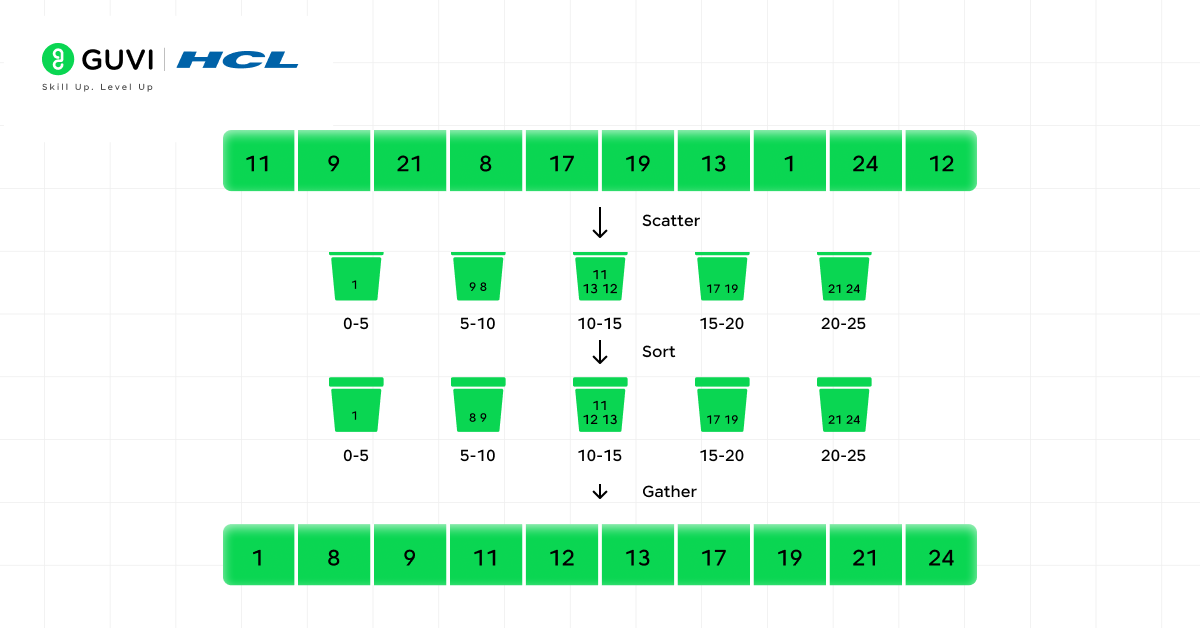
Bucket Sort is a distribution-based sorting algorithm from the world of data structures and algorithms. That means it relies on how the values are spread out rather than comparing every element to every other element.

Bucket Sort doesn’t think the same way traditional comparison-based algorithms do. Instead of comparing pairs of elements one at a time, it groups elements into different “buckets” based on their value range. Once the data is organized into buckets, each bucket is sorted individually, and then all the buckets are combined back in order to get the final result.

Here’s the basic process:

1. Divide the input into several buckets.
2. Distribute each element into the appropriate bucket based on its value.
3. Sort each bucket individually.
4. Concatenate all buckets to produce the final sorted array.

The key insight is that sorting many small groups is often faster than sorting one large group.

Why Bucket Sort Works

Imagine you’re sorting students by their exam scores out of 100. Instead of sorting the entire list directly, you could create buckets such as 0–9, 10–19, 20–29, and so on. 

Each student goes into the bucket that matches their score range. Once the scores are bucketed, each group is already partially organized by range. Sorting inside each bucket becomes easier and faster.

This approach leverages knowledge about the distribution of data. If you know your values fall within a certain range and are somewhat evenly spread out, Bucket Sort becomes extremely efficient.

Step-by-Step Breakdown of the Bucket Sort Algorithm

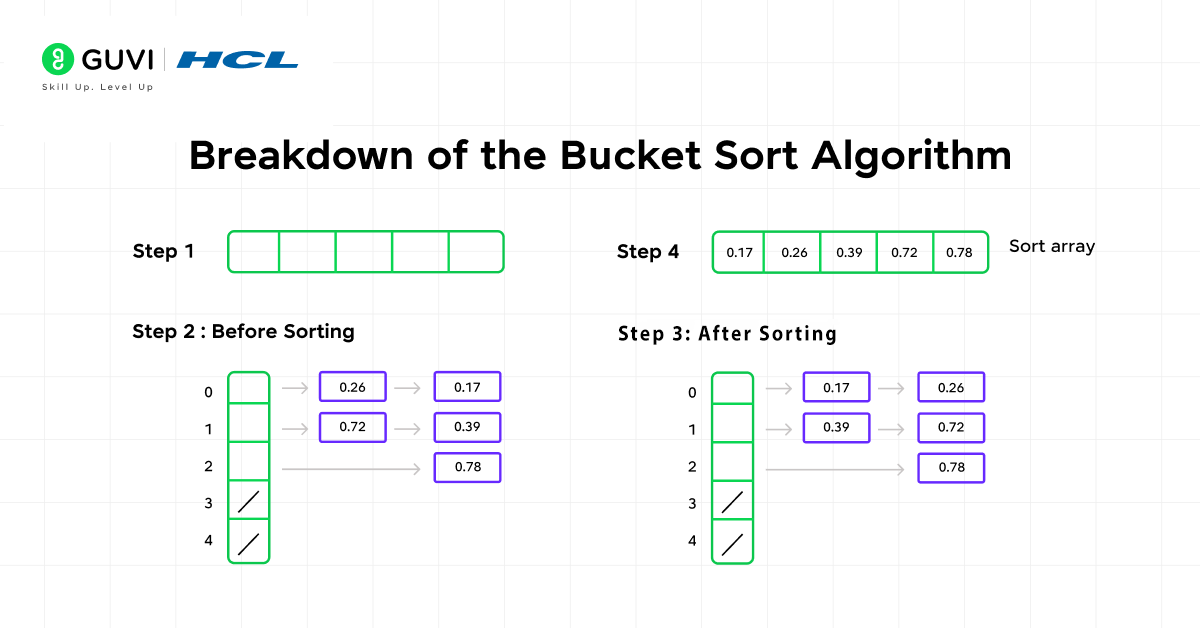
Understanding the idea is helpful, but let’s look at how the algorithm actually executes.

Step 1: Create Buckets

You predefine a certain number of buckets. Each bucket represents a specific range of values. The number of buckets is important; you don’t want them too large or too small.

Step 2: Distribute the Elements

Each element from the input goes into a specific bucket based on its value. The mapping from value to bucket is usually done by a simple formula.

Step 3: Sort Each Bucket

Once all elements are distributed, each bucket is sorted individually. Because buckets are smaller than the original list, sorting them is faster.

Step 4: Merge the Buckets

Finally, the sorted buckets are concatenated to form the fully sorted array.

That’s the core of the bucket sort algorithm. It’s conceptually simple once you see it laid out this way.

If you want a platform that actually teaches DSA in a structured, beginner-friendly way while also giving you practical coding experience, consider enrolling in HCL GUVI’s DSA for Programmers Course that is designed specifically for learners who want clarity instead of confusion. It explains concepts in simple terms and guides you from basics to advanced topics step-by-step. 

Basic Python Implementation of Bubble Sort

Let’s start with the most common bucket sort scenario in Python, sorting floating-point numbers in the range 0 to 1.

def bucket_sort(arr):

    if len(arr) == 0:

        return arr

    # 1. Create buckets

    buckets = [[] for _ in range(len(arr))]

    # 2. Distribute elements

    for num in arr:

        index = int(num * len(arr))  # Determine bucket index

        buckets[index].append(num)

    # 3. Sort each bucket

    for i in range(len(buckets)):

        buckets[i].sort()

    # 4. Concatenate buckets

    sorted_arr = []

    for bucket in buckets:

        sorted_arr.extend(bucket)

    return sorted_arr

data = [0.42, 0.32, 0.23, 0.52, 0.25, 0.47]

print(bucket_sort(data))

This example illustrates the purest form of bucket sort. It assumes all values are between 0 and 1 and maps them directly to buckets by scaling.

Know how Python helps DSA to a great extent by reading – DSA with Python: Understand the Foundations of Coding

But What If the Values Are Integers?

Bucket sort can handle integers, too, but we need to think differently. Instead of multiplying values to map them into buckets, we can use bucket ranges.

def bucket_sort_integers(arr, bucket_size=5):

    if len(arr) == 0:

        return arr

    min_value = min(arr)

    max_value = max(arr)

    bucket_count = (max_value - min_value) // bucket_size + 1

    buckets = [[] for _ in range(bucket_count)]

    for num in arr:

        index = (num - min_value) // bucket_size

        buckets[index].append(num)

    sorted_arr = []

    for bucket in buckets:

        sorted_arr.extend(sorted(bucket))

    return sorted_arr

data = [42, 32, 23, 52, 25, 47, 15, 10]

print(bucket_sort_integers(data))

Here, we’re grouping values based on ranges. Each bucket handles a slice of the number line.

Why Use Insertion Sort Inside Buckets?

You might wonder why insertion sort is used inside buckets, and that’s because insertion sort is often chosen inside buckets. After all, buckets usually contain only a few elements. For small datasets, insertion sort is efficient, simple, and stable. 

But you’re not locked into using insertion sort. You can sort buckets using quicksort, mergesort, or even Python’s built-in sorted() if that’s easier. The algorithm is flexible.

Time and Space Complexity Analysis of Bucket Sort

The time complexity of bucket sort depends on how the elements are distributed.

Best case: All elements are spread evenly across buckets, and each bucket has just a few elements. Sorting each bucket is fast, leading to near O(n + k) time, where k is the number of buckets.

Average case: Similar to the best case, assuming uniform distribution. The algorithm remains efficient.

Worst case: All elements land in the same bucket. Now, you’re essentially just sorting a normal list using whatever algorithm you used internally, often O(n²) if you used insertion sort.

Space Complexity

Bucket sort requires additional memory for the buckets. In total, it uses about O(n + k) space, where n is the number of input elements and k is the number of buckets. This is more memory than in-place sorting algorithms like quicksort.

Learn more about complexities in DSA by reading our blog – Understanding Complexity Analysis in Data Structures

When Bucket Sort Works Best?

Bucket sort shines when:

• The data is uniformly distributed.
• You know the range of the input in advance.
• You’re dealing with floating-point numbers.
• Speed is critical, and near-linear time is needed.
• The dataset is large enough that optimizing makes a difference.

When those conditions are met, bucket sort can outperform many comparison-based sorting algorithms.

When Bucket Sort Falls Short?

It’s not a universal solution. Bucket sort struggles when:

• Data is heavily skewed or clustered.
• The distribution is unknown.
• The range of values is extremely large.
• Memory usage must be minimized.
• Predictable performance is required.

In these cases, merge sort or quicksort might be more appropriate.

Comparing Bucket Sort with Other Sorting Algorithms

Bucket sort is not like bubble sort, merge sort, or quicksort. Those are comparison-based algorithms. They look at two elements at a time and decide which goes first. Bucket sort, on the other hand, uses value ranges to organize elements, reducing the need for comparisons entirely.

Compared to merge sort or quicksort, bucket sort can run in linear time, which is better than O(n log n). However, it only achieves that speed when the data meets certain conditions. Merge sort and quicksort are reliable across a wider range of inputs.

Bucket Sort vs Radix Sort vs Counting Sort

These three algorithms are often discussed together because they’re all non-comparison sorting methods.

• Counting Sort counts how many times each value appears. It’s extremely fast but only works when the range of values is small.
• Radix Sort sorts numbers digit by digit, from least significant digit to most. It uses counting sort internally, but works better for larger numbers.
• Bucket Sort groups values into ranges and sorts within each range. It’s more flexible than counting sort and easier to understand than radix sort, but it depends heavily on distribution.

Real-World Use Cases of Bucket Sort

Bucket sort might not be the first algorithm you code in production, but it appears in many places indirectly. Systems that group or partition data before sorting often use bucket sort techniques internally.

It’s used in these scenarios:

• Sorting floating-point numbers (0 to 1)
• Distributing students by score ranges
• Parallel processing (buckets can be processed concurrently)
• Graphics and computational geometry
• Hashing-based tasks
• Load balancing/grouping tasks

If you want to read more about how DSA paves the way for effective coding and its use cases, consider reading HCL GUVI’s Free Ebook: The Complete Data Structures and Algorithms Handbook, which covers the key concepts of Data Structures and Algorithms, including essential concepts, problem-solving techniques, and real MNC questions

Pros and Cons of Bucket Sort

Bucket sort brings speed and simplicity when conditions align. It’s naturally stable and highly parallelizable. It can outperform O(n log n) algorithms in specific scenarios, which is rare. Here is a quick run-through of the pros and cons

Advantages

• It can be faster than O(n log n)
• It is especially good for floating-point data
• It is easy to implement compared to others
• It is highly parallelizable
• It is more stable than other sorting algorithms.

Disadvantages

• It requires an understanding of data distribution
• The bucket size selection is tricky and hard at times
• The worst-case can hit as low as O(n²)
• It uses extra memory due to the bucket storage
• It is not a universal-purpose like QuickSort

It’s not a general-purpose sort, but when it fits the data, it’s incredibly effective.

Choosing the Right Number of Buckets

Bucket count is one of the most important design decisions. Too few buckets, and they become overloaded. Too many, and memory is wasted.

A common rule is to create as many buckets as elements, or sometimes the square root of n. But in practice, you choose bucket sizes based on data distribution, not hard rules.

Put it simply:

Too few buckets? Each bucket becomes large → slow.

Too many buckets? Most buckets are empty → wasted space.

Rule of thumb: Use the number of buckets ≈ number of elements (or √n in some implementations).

Common Mistakes to Avoid

• Beginners often assume bucket sort works for every dataset, which leads to disappointing results. 
• Another frequent mistake is picking a poor bucket size or count, causing uneven distribution. Some forget to sort buckets entirely. 
• Negative numbers can also cause issues if not handled properly. And finally, some people expect linear time performance without checking whether the input is uniform.

Understanding limitations is as important as knowing the steps.

Handling Negative Numbers in Bucket Sort

Bucket sort can handle negative numbers easily, as long as you adjust the mapping. One way is to find the minimum value in the list and shift all elements by subtracting that minimum. Once shifted, everything becomes non-negative and can be bucketed normally. After sorting, you shift the values back.

In short:

• Find min value
• Shift all elements (num – min)
• Apply bucket sort
• Shift back if needed

It’s a simple trick, but many forget it.

Bucket Sort in Interviews

Interviewers rarely ask you to code bucket sort from memory, but they love testing whether you understand where it fits. They might ask you to explain the algorithm, compare it with radix or counting sort, or describe when it’s efficient.

Frequently Asked Interview Questions:

• Explain bucket sort.
• Where is bucket sort efficient?
• How is it different from counting or radix sort?
• Why isn’t it used everywhere?
• What happens if all elements go into one bucket?
• How to choose the number of buckets?

Pro tip: Interviewers care more about when you’d use it than writing exact code.

Also learn about the top DSA questions that interviewer asks commonly in interviews by reading – 30 Sureshot DSA Interview Questions And Answers

Remember that bucket sort isn’t just a sorting algorithm. It teaches a principle: sometimes you can solve a problem faster by grouping data strategically rather than comparing everything directly.

If you’re serious about mastering DSA in software development and want to apply it in real-world scenarios, don’t miss the chance to enroll in HCL GUVI’s IITM Pravartak and MongoDB Certified Online AI Software Development Course. Endorsed with NSDC certification, this course adds a globally recognized credential to your resume, a powerful edge that sets you apart in the competitive job market.

Conclusion

In conclusion, bucket sort is like organizing books into shelves before sorting each shelf. It’s not always the best approach, but when the books are already roughly grouped, it makes everything faster. 

The algorithm rewards you for understanding your input. It’s a great example of how knowing your data can lead to smarter solutions than simply applying generic tools.

Even if you never use bucket sort directly in production, the way it approaches sorting will improve how you think about efficiency, structure, and data distribution.

FAQs

1. What is the Bucket Sort algorithm?

Bucket Sort is a distribution-based sorting algorithm that divides elements into multiple buckets based on value ranges, sorts each bucket individually, and then merges them to produce the final sorted list.

2. When should I use Bucket Sort?

Use bucket sort when the input data is uniformly distributed and you know the value range in advance. It’s especially efficient for sorting floating-point numbers or grouped numerical data.

3. What is the time complexity of Bucket Sort?

Best and average case time complexity is O(n + k), where k is the number of buckets. In the worst case, when all elements fall into one bucket, it can degrade to O(n²).

4. Is Bucket Sort better than Quick Sort or Merge Sort?

It can be faster than O(n log n) algorithms like quicksort or mergesort, but only when the data is evenly distributed. For general-purpose sorting, quicksort or mergesort is more reliable.

5. Is Bucket Sort stable and in-place?

Bucket sort is stable if the sorting inside buckets is stable (like insertion sort). It is not in-place because it requires extra memory for buckets.